[analyse] fonctions de plusieurs variables

[parisien75]

Bonjour à tous.
Est ce que si une fonction à deux variables
f : A -> R
(x,y)-> f(x,y)

definie sur un sous ensemble A de R² admet des limites finies aux points ou elles n'est pas continue et en l'inf est bornée?


Merci de vos reponses.

[tize]

Il me semble bien que oui, si tend vers une limite finie quand . Il existe alors A>0, C>0 tq pour , on a . Reste à montrer que f est bornée sur . Si ça n'était pas le cas alors il existerait une suite de A tq mais puisque E est compact on peut extraire de une sous suite et

[Franck75019]

Question existentielle..... :lol4:

[parisien75]

Bonsoir
Je ne vois pas pourquoi c'est bornée sur E?
Merci d'avance

[fahr451]

Bonjour à tous.
Est ce que si une fonction à deux variables
f : A -> R
(x,y)-> f(x,y)

admet des limites finies aux points ou elles n'est pas continue

Merci de vos reponses.

donc aux points de adh(A) \ A

il suffit alors d e prolonger f à tout adh(A) par continuité

puis comme l'a dit tize en dehors d 'une certaine boule B fermée f est bornée, et sur le compact adh A inter B f étant continue également

[parisien75]

Merci bcp pour vos réponses.

J'ai une autre question.

Soit une fonction a deux variables definies sur un sous ensemble 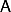(par ex 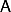= ]a,[) de ².

On cherche à determiner si cette fonction est bornée ou non.

Sur l'intervalle où est continue, donc il n'y a pas de probleme. La fonction est bornée.

Mais si par exemple, lorsque , la fonction admet comme limite (pour une direction choisie) l' , pourquoi peut on alors affirmé que la fonction n'est pas bornée?
Deux cas se presente :

**soit la fonction en l' admet pour tout direction l' comme limite. -> dans ce cas non bornée.

**soit la limite en l' de f n'existe pas dans le cas où on trouve une direction de(x,y) allant vers l' ou la limite de f n'est pas l' . -> dans ce cas non bornée

Dans le deuxieme cas, je ne vois pas pourquoi f est non bornée.

Merci d'avance.

[parisien75]

Personne n'a d'idée?

[fahr451]

bonsoir

je ne comprends pas trop ta question

bornée

il existe M tel que pour tout (x,y) dans Df l f(x,y) l =< M;

si dans une certaine direction f tend vers l'infini elle n'est donc pas bornée non?

[parisien75]

En fait, ma question c'est :

Si dans une certain direction (lorsque par exemple tend vers l') , la limite de f est + et dans une autre direction, la limite est differente de + (ce qui veut dire que la limite en + n'existe pas, non?)
alors pourquoi peut on conclure que n'est pas bornée?