Fonctions intégrables au sens de Riemann

[manou11]

Bonjour à tous,
je suis en L1 Maths et dans le programme d'Analyse nous travaillons sur l'intégration et ici en particulier sur les fonctions en escalier/réglées et intégrables au sens de Riemann.
Je dois résoudre un exercice mais je ne vois pas comment procéder.
Voici l'énoncé :

Soit f : [a, b] → R une fonction réglée.
(1) Montrer qu’il existe une suite de fonctions en escalier (ϕn) telles que
lim n→+∞ ϕn(x) = f(x), pour tout x ∈ [a, b].
(2) Montrer que cette suite (ϕb) peut être prise en dessous de f ou bien par dessus.
(3) Donner une idée pour la construction de cette suite quand f : [0, 1] → R est définie par f(x) = x

Je sais que toute fonction en escalier est réglée mais est ce que cela peut me servir ici ?

Merci d'avance du temps que vous me consacrerez, je serais très reconnaissante d'obtenir de l'aide.

[mathelot]

bonsoir,


question 3

on définit la suite de fonction , définies sur [0;1] par



l'intégrale de vaut:



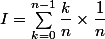
il reste à calculer I et à montrer que sa limite est 1/2 quand n tend vers l'infini.

remarque: I s'appelle une "somme de Darboux" minorante de f.

[manou11]

Merci pour votre aide, je vais m'inspirer de cela pour répondre à la question.
Bonne soirée à vous

bonsoir,


question 3

on définit la suite de fonction , définies sur [0;1] par



l'intégrale de vaut:



il reste à calculer I et à montrer que sa limite est 1/2 quand n tend vers l'infini.

remarque: I s'appelle une "somme de Darboux" minorante de f.