Je bloque sur un exo sur les fonctions de classes
Voiçi l'énoncé :
Soit
Il est clair que :
Montrer que :
où
Povez vous m'expliquer quel chemin faut-t-il suivre pour le prouver ?
Merci infiniment !
Fonctions infiniment dérivables
7 messages
- Page 1 sur 1
Fonctions infiniment dérivables
par barbu23 » 14 Fév 2009, 23:37
Bonsoir à tous :
Je bloque sur un exo sur les fonctions de classes
:
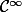
Voiçi l'énoncé :
Soit
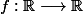
une fonction définie par :
 = e^{\frac{1}{x}} $)
si : 
.
 = 0 $)
si 
.
Il est clair que :
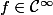
sur 
.
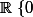
Montrer que :
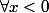
: }(x) = P_{n}(\frac{1}{x}) e^{\frac{1}{x}} $)
où
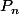
est un polynôme défini par la suite réccurente suivant :
 = 1 $)
 = - X^{2} ( P_{n}^{'}(X)+P_{n}(X)) $)
Povez vous m'expliquer quel chemin faut-t-il suivre pour le prouver ?
Merci infiniment !
Je bloque sur un exo sur les fonctions de classes
Voiçi l'énoncé :
Soit
Il est clair que :
Montrer que :
où
Povez vous m'expliquer quel chemin faut-t-il suivre pour le prouver ?
Merci infiniment !
par ThSQ » 14 Fév 2009, 23:51
barbu23 a écrit:réccurente
La réponse est dans la question non ?
( bon perso je mettrais un 'c' et deux 'r' à récurrente
)par barbu23 » 14 Fév 2009, 23:56
Non, la question est de montrer que :
 = P_{n}(\frac{1}{x}) e^{\frac{1}{x}} $)
Et c'est là que je bloque ! :hum: :we:
Et c'est là que je bloque ! :hum: :we:
par nuage » 15 Fév 2009, 00:02
Salut,
Essayes de calculer les dérivées successives de
pour 
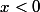
Pour commencer :
=\frac{-1}{x^2^}e^{\frac1{x}})
![](https://latex.ilemaths.net/ile_TEX.cgi?f" (x)= \frac2{x^3}e^{\frac1{x}}+\frac1{x^4}e^{\frac1{x}})
et regarde comment se fait le calcul.
Essayes de calculer les dérivées successives de
Pour commencer :
et regarde comment se fait le calcul.
par barbu23 » 15 Fév 2009, 01:18
Bonsoir à tous :
Merci por vos reponses !
Et si je dérive directement pet être que ça marchera bien !
}(x) = (P_{n}(\frac{1}{x}) e^{\frac{1}{x}})'=-(\frac{1}{x})^{2}) P_{n}'(\frac{1}{x}) e^{\frac{1}{x}} - \frac{1}{x^{2}} P_{n}(\frac{1}{x}) e^{\frac{1}{x}} = - \frac{1}{x^{2}}(P'_{n}(\frac{1}{x}) +P_{n}(\frac{1}{x}) e^{\frac{1}{x}} = P_{n+1}(\frac{1}{x}) e^{\frac{1}{x}} $)
Et ben voilà ! c'est fait ! comme je l'ai prevu ça marche ! :zen: :we:
Cordialement !
Merci por vos reponses !
Et si je dérive directement
Et ben voilà ! c'est fait ! comme je l'ai prevu ça marche ! :zen: :we:
Cordialement !
par Ptiboudelard » 16 Fév 2009, 13:00
C'est un produit de deux fonctions. Tu peux donc utiliser la formule de Leibniz. Non ?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :