Fonctions holomorphes

[oggar]

Bonjour, je suis bloqué sur cet exercice, si vous pouvez m’aider.

1) Déterminer les fonctions holomorphes sur qui vérifient :

2) soit une fonction continue sur le disque fermé telle que .

2-1) Déterminer si f est holomorphe dans le disque ouvert .

2-2) Vérifie que pour tout

3) Déterminer toutes les fonctions entières sur telles que : ,


Pour la question 3) j’ai considéré la fonction

donc :

On fait tendre vers l’infini donc tends vers , le principe des zéros isolés confirme que est non nul, ceci est possible que si donc .

Ici on voit que et la fonction satisfait la condition donc .

Mais ce n’est pas rigoureux de dire que implique que .

[aviateur]

On dirait qu'il y a 3 exo différents et je suis assez interrogatif sur le 2.!!!!

Le 1 a pour uniques solutions

Le 3 tu as quasiment la réponse, en effet les conditions imposent que

[oggar]

Bonjour aviateur et merci pour votre réponse,
Pour le 1) Peut-tu m'expliquer comment tu as arrivé à cette solution

[oggar]

Bonjour,

Comme la fonction est holomorphes sur , j’ai donc posé :

Cela donne :

La limite de cette expression vaut 3, cela veut dire que :



Les solutions de cette équation différentielle sont :

Donc :

Je ne trouve pas la même salutation que toi

[aviateur]

Oui est non.
Bon d'abord, j'ai interverti f et f' (tout se passe comme si j'avais remplacé 3 par -3).
Donc j'ai corrigé il faut changer le signe de mes solutions. Mais mis à part cela j'ai bien donné toutes les solutions.
Maintenant ta solution fait partie de l'ensemble des solutions que j'ai donné (après correction).
Mais il te manque des solutions.
Revois ton calcul d'ailleurs je ne comprends pas h et g ?

[oggar]

C’est juste une erreur d’inattention h c’est bien g.

[aviateur]

corrigé..

[aviateur]

Et l'exercice 2, tu as corrigé l'énoncé? Car je trouve pas mal ces petits exos sur les fonctions holomorphes qui fait réfléchir les débutants.
Je suis certain que ça doit être intéressant mais je n'arrive pas à deviner ce que ça pourrait être.

[oggar]

Je pense aussi qu'il y a une erreur dans l'énoncé de la question 2) , il s'agit de l'exercice d'un TD , j'ai envoyé un mail à l'enseignant.

[oggar]

j'ai un autres exercices dans le meme chapitres ( les fonctions holomorphes) , mais j'aimerai d'abord terminer la question 1) avant de le poster.

J’ai eu l’habitude de résoudre une équation différentielle sur , je n’ai pas vraiment compris comment je fais le passage pour que toutes les solutions soient holomorphes.

[aviateur]

De toute façon ça change rien pour l'équa-diff.
Par exemple, si tu résous y'+y=0 , la solution générale est Ce^{-x}, C appartenant à R. SI tu mets C complexe tu obtiens toutes les solutions sur C.
¨

[oggar]

Pour , j’ai trouvé une solution de l’équation homogène et une solution particulière .
comment je vais mettre C complexe ?

Je ne vois pas comment je vais mettre C complexe ?

[oggar]

Je n’arrive vraiment pas à voir comment tu as trouvé ces solutions.

[aviateur]

Bon je reprends car j'avais pas écrit les choses comme toi et donc il y a une remarque que j'ai fait et qui est fausse.
Alors avec tes notations on a f(z)=a+bz+z^2 h(z) holomorphe.
La condition implique que -b + 2 h(z) - z + z h'(z)=3
La résolution de l'équation différentielle donne bien , avec
solution valable pour tout

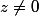
Remarque 1. La procédure de résolution sur est la même que (rien ne change à la théorie).

Remarque 2. Ce qui change par rapport à ma remarque précédente que j'ai supprimée (perso je n'avais pas le même problème) c'est que parmi les solution obtenues certaine ne sont pas définies en z=0.
Alors avec un développement en z=0 , tu vas trouver une seule valeur de C compatible.
En remplaçant C tu va trouver une famille de solutions qui dépend des paramètres a et b.
Normalement tu vas retrouver le même que moi (peut être à la différence près que mes paramètres alpha et beta sont peut être différent, j'ai un peu oublié ma démarche d'hier).

[oggar]

J’ai corrigé mon erreur de frappe c’est (b+3) et pas ( b+z) :

Donc les solutions sont : , avec

Donc :



Vérification :

, alors

Et

[oggar]

Tu parles d’un développement limité ou d’un développement en série entière en z=0 ?

Comment va-t-on trouver cette valeur de C compatible ?
J’ai essayé, mais je n’arrive pas

[aviateur]

Non il ne faut plus tenir compte de cette remarque. Tout est OK maintenant
Si je comprends bien tu avais fait une (petite) erreur. Alors h était holomorphe seulement pour une valeur de C
(à voir avec un DL ou DL en série de Laurent). Mais ça on n'a pas à le faire avec l'erreur corrigée
Perso j'avais pas ce pb non plus donc + de pb.

[aviateur]

Concernant le pb 3. je suis d'accord on a bien h(z)=1/2 i puisque tu as montré que h vérifie 2h(z)+zh'(z)-i=0.