Bonsoir,
Je bloque certainement sur une question très simple mais je n'y arrive pas.
Comment savoir si une fonction est holomorphe ?
Exemple : f(z) = log(z) avec z = x+iy
Je connais les conditions de Cauchy mais je ne sais comment les appliquer.
Merci de votre aide.
Fonctions Holomorphes
10 messages
- Page 1 sur 1
par MouLou » 30 Sep 2015, 19:11
Oui en effet! c'est pas le meilleur exemple pour commencer!
Pour les conditions de Cauchy-Riemann, si tu connais le calcul différentiel, tu regardes une fonction de
dans comme un fonction de 
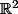dans 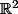:=(f_{1}(x,y),f_{2}(x,y))$$)
Alors ta fonction est holomorphe en un point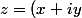\in \mathbb{C})
si elle est différentiable et que sa différentielle est -linéaire.
Cela siginifie que si tu regardes la matrice de la différentielle, elle est de la forme (a,b;-b,a), (a et a dans la diagonale). c'est a dire=\frac{df_{2}}{dy}(z))
et =-\frac{df_{2}}{dx}(z))
.
Prenons un exemple:=e^{z}=(e^{x}cos(y),e^{x}sin(y)))
avec z=x+iy
alors:
=e^{x}cos(y))
=-e^{x}sin(y))
=e^{x}sin(y))
=e^{x}cos(y))
.
Donc on peut en déduire que f est holomorphe en tout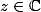
Pour les conditions de Cauchy-Riemann, si tu connais le calcul différentiel, tu regardes une fonction de
Alors ta fonction est holomorphe en un point
Cela siginifie que si tu regardes la matrice de la différentielle, elle est de la forme (a,b;-b,a), (a et a dans la diagonale). c'est a dire
Prenons un exemple:
alors:
Donc on peut en déduire que f est holomorphe en tout
par Robot » 30 Sep 2015, 19:37
Henri12 a écrit:Quelles informations souhaites tu en plus :/ ?
Sur quel ouvert de
Une fois ceci précisé de manière cohérente, l'holomorphie ne pose pas de problème puisque
par Henri12 » 30 Sep 2015, 20:26
@MouLou Merci pour ton exemple concret j'ai bien compris le principe 
@Robot U un ouvert de C et f une fonction dans C. Après pour la détermination du logarithme je vois pas trop où tu veux en venir :/
@Robot U un ouvert de C et f une fonction dans C. Après pour la détermination du logarithme je vois pas trop où tu veux en venir :/
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :