Fonctions génératrices
7 messages
- Page 1 sur 1
Re: Fonctions génératrices
Ton expérience aléatoire n'est quasiment pas expliquée .
Soit précis s'il te plait . Pour être aidé , il faut d'abord être compris .
Soit précis s'il te plait . Pour être aidé , il faut d'abord être compris .
Re: Fonctions génératrices
Bonjour,
la fonction génératrice (cf wikipédia par exemple https://fr.wikipedia.org/wiki/Fonction_ ... lit%C3%A9s ) est un outil pour l'étude des variables aléatoires. A une variable aléatoire X (entière) donnée on associe une fonction
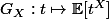
c'est une fonction de t (ou de z dans ton exemple) qui a diverses propriété que l'on peut étudier. L'une des plus simple est de calculer les moments (espérance, espérance du carré, etc...) d'une variable aléatoire a partir de la fonction génératrice.
Pour aller plus loin il faudrait des détails sur ton problème...
la fonction génératrice (cf wikipédia par exemple https://fr.wikipedia.org/wiki/Fonction_ ... lit%C3%A9s ) est un outil pour l'étude des variables aléatoires. A une variable aléatoire X (entière) donnée on associe une fonction
c'est une fonction de t (ou de z dans ton exemple) qui a diverses propriété que l'on peut étudier. L'une des plus simple est de calculer les moments (espérance, espérance du carré, etc...) d'une variable aléatoire a partir de la fonction génératrice.
Pour aller plus loin il faudrait des détails sur ton problème...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Fonctions génératrices
Bonjour,
je crois que le problème que se pose ruslan est le suivant :
si je lance une pièce indéfiniment, et que je regarde l'instant de première apparition de la séquence fixée "PFFFP",
- combien de lancers devrais-je attendre (en moyenne) ?
- peut - on donner un intervalle de confiance à 90 % (resp. 95%, 99%) de ce nombre de lancers, c'est à dire un nombre de lancers qui m'assure d'une probabilité de 90% (resp. 95%, 99%) de réaliser cette séquence?
- plus généralement, toute question sur la loi de la variable aléatoire T, à valeurs dans N* de première réalisation de cette séquence (on parle de temps d'attente)
C'est une question intéressante, et je te conseille au niveau de la L1 plusieurs axes de travail:
- axe théorique sur un problème simplifié. Si la séquence est (beaucoup) plus simple, comme "P" ou "F", peux-tu donner la loi de la v.a. T ?
Même question si la séquence est "FF", "FP", "PP", "PF"
- axe pratique/simulation de statistique empirique sur des échantillons avec R ou Python (par exemple) : tu simules des échantillons de longueur N (= 10000 par exemple) et tu recherches dedans la première apparition de ta séquence dans l'ordre.
En traitant un grand nombre d'échantillons, tu peux faire des statistiques et ainsi calculer des statistiques empiriques sur la variable aléatoire T.
Pour compléter le message de Sylviel : la fonction génératrice que tu mentionnes H(z)=pz+(1-p) est celle d'une loi de Bernoulli de paramètre p.
je crois que le problème que se pose ruslan est le suivant :
si je lance une pièce indéfiniment, et que je regarde l'instant de première apparition de la séquence fixée "PFFFP",
- combien de lancers devrais-je attendre (en moyenne) ?
- peut - on donner un intervalle de confiance à 90 % (resp. 95%, 99%) de ce nombre de lancers, c'est à dire un nombre de lancers qui m'assure d'une probabilité de 90% (resp. 95%, 99%) de réaliser cette séquence?
- plus généralement, toute question sur la loi de la variable aléatoire T, à valeurs dans N* de première réalisation de cette séquence (on parle de temps d'attente)
C'est une question intéressante, et je te conseille au niveau de la L1 plusieurs axes de travail:
- axe théorique sur un problème simplifié. Si la séquence est (beaucoup) plus simple, comme "P" ou "F", peux-tu donner la loi de la v.a. T ?
Même question si la séquence est "FF", "FP", "PP", "PF"
- axe pratique/simulation de statistique empirique sur des échantillons avec R ou Python (par exemple) : tu simules des échantillons de longueur N (= 10000 par exemple) et tu recherches dedans la première apparition de ta séquence dans l'ordre.
En traitant un grand nombre d'échantillons, tu peux faire des statistiques et ainsi calculer des statistiques empiriques sur la variable aléatoire T.
Pour compléter le message de Sylviel : la fonction génératrice que tu mentionnes H(z)=pz+(1-p) est celle d'une loi de Bernoulli de paramètre p.
Re: Fonctions génératrices
Ce type de pb se résout facilement par l'espérance conditionnelle et de petits arbres pondérés:
Je note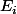 l'esperance conditionnelle du nombre de coups sachant que i composantes de la séquence sont réalisés . Par exemple
l'esperance conditionnelle du nombre de coups sachant que i composantes de la séquence sont réalisés . Par exemple 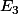 est l'espérance conditionnelle du nombres de coups nécessaires à la réalisation de la sequence sachant que la séquence PFF est déjà réalisée .
est l'espérance conditionnelle du nombres de coups nécessaires à la réalisation de la sequence sachant que la séquence PFF est déjà réalisée .
On cherche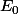 .
.
Si le premier lancer donne F , tout est à refaire . L'esperance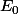 est augmentée de 1 mais avec la probabilité 1/2 .
est augmentée de 1 mais avec la probabilité 1/2 .
Si le premier lancé donne P , on est en bonne voie . L'esperance est alors de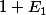 mais avec une probabilité de 1/2 .
mais avec une probabilité de 1/2 .
En resumé , on a :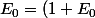\frac{1}{2}+(1+E_1)\frac{1}{2})
On en déduit que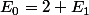 .
.
On déduit de même que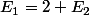 ,
, 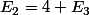 ,
, 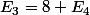 et enfin que
et enfin que 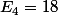 .
.
On en déduit que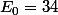 .
.
Attention à la simulation car toutes les séquences de 5 lancers n'ont pas la même espérance de première réalisation .Il est facile de calculer que celle de la séquence PP est égale à 6 , alors que celle de la séquence PF est égale à 4 . Il faut donc simuler exatement avec la séquence PFFFP .
Je note
On cherche
Si le premier lancer donne F , tout est à refaire . L'esperance
Si le premier lancé donne P , on est en bonne voie . L'esperance est alors de
En resumé , on a :
On en déduit que
On déduit de même que
On en déduit que
Attention à la simulation car toutes les séquences de 5 lancers n'ont pas la même espérance de première réalisation .Il est facile de calculer que celle de la séquence PP est égale à 6 , alors que celle de la séquence PF est égale à 4 . Il faut donc simuler exatement avec la séquence PFFFP .
Re: Fonctions génératrices
Je n'ai pas été assez précis:
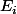 est l'espérance conditionnelle du nombre de coups restants necessaires à la réalisation de la séquence PFFFP sachant que ses i premières composantes sont deja réalisées .
est l'espérance conditionnelle du nombre de coups restants necessaires à la réalisation de la séquence PFFFP sachant que ses i premières composantes sont deja réalisées .
Re: Fonctions génératrices
Je vous remercie énormément pour vos réponses qui m'ont beaucoup aidé ! Mon sujet est justement très vague, ma seule consigne est " Combien de fois faut-il lancer une pièce pour obtenir PFFFP" et un document parlant entre autre de fonctions génératrices, vos réponses mon donc donnés beaucoup de pistes !
Mais j'avoue que j'ai toujours du mal avec les fonctions génératrices .. J'arrive pas à visualiser le rôle de z ( ou t comme je le vois la plupart du temps sur internet ). Je crois avoir compris que z peut prendre différentes valeurs entre -1 et 1, mais je comprends pas très bien ce que c'est concrètement. Est-ce que ce serait possible d'avoir un exemple pour que je comprenne bien son rôle ? ( Parce que quand j'utilise des fonctions génératrices je remplace par 1 dans ma tête pour "ignorer" le fait que je comprenne pas son rôle )
Mais j'avoue que j'ai toujours du mal avec les fonctions génératrices .. J'arrive pas à visualiser le rôle de z ( ou t comme je le vois la plupart du temps sur internet ). Je crois avoir compris que z peut prendre différentes valeurs entre -1 et 1, mais je comprends pas très bien ce que c'est concrètement. Est-ce que ce serait possible d'avoir un exemple pour que je comprenne bien son rôle ? ( Parce que quand j'utilise des fonctions génératrices je remplace par 1 dans ma tête pour "ignorer" le fait que je comprenne pas son rôle )
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
