Fonctions de deux variables
14 messages
- Page 1 sur 1
Fonctions de deux variables
Bonjour,
Je suis nouveau sur ce forum et j'esperais que je pourrai avoir un petit coup de pouce sur ces quelques affirmations :
*Supposons que f(x, y) est une fonction de deux variables admettant des dérivées partielles telle que pour tout (x, y) on a ;)f/;)x(x, y);)1 et ;)f/;)y (x, y) ;) 0. Alors f(2, 1) ;) f(0, 0) + 2.
*Supposons que f(x, y) est une fonction de deux variables admettant un vecteur gradient tel que ||;););) Gradf(x, y)|| ;) 1 en tout point (x, y) du plan. Alors f(1, 1) ;) f(0, 0) + ;)2.
*Soit P : R ;) R un polynôme et soit f(x, y) = P(x^2 + y^2). Alors f(x, y) est constante sur chaque cercle de centre (0, 0) et le vecteur ;);););) Gradf(2,3) est de la forme (2t, 3t) (pour un réel t convenablement choisi).
*Les solutions (x, y) de léquation (2x+y;)1)/(1+x^2y^4) = 0 sont données par y=1;)2x, x ;) R quelconque. Donc le gradient de f(x, y) = (2x+y;)1)(1+x^2y^4) en tout point de la droite déquation y = 1;)2x est dans la direction de (;)1,2).
Je suis nouveau sur ce forum et j'esperais que je pourrai avoir un petit coup de pouce sur ces quelques affirmations :
*Supposons que f(x, y) est une fonction de deux variables admettant des dérivées partielles telle que pour tout (x, y) on a ;)f/;)x(x, y);)1 et ;)f/;)y (x, y) ;) 0. Alors f(2, 1) ;) f(0, 0) + 2.
*Supposons que f(x, y) est une fonction de deux variables admettant un vecteur gradient tel que ||;););) Gradf(x, y)|| ;) 1 en tout point (x, y) du plan. Alors f(1, 1) ;) f(0, 0) + ;)2.
*Soit P : R ;) R un polynôme et soit f(x, y) = P(x^2 + y^2). Alors f(x, y) est constante sur chaque cercle de centre (0, 0) et le vecteur ;);););) Gradf(2,3) est de la forme (2t, 3t) (pour un réel t convenablement choisi).
*Les solutions (x, y) de léquation (2x+y;)1)/(1+x^2y^4) = 0 sont données par y=1;)2x, x ;) R quelconque. Donc le gradient de f(x, y) = (2x+y;)1)(1+x^2y^4) en tout point de la droite déquation y = 1;)2x est dans la direction de (;)1,2).
Salut !
Qu'as-tu fait pour le moment : expose tes idées :++:
yanisdourge a écrit:Bonjour,
Je suis nouveau sur ce forum et j'esperais que je pourrai avoir un petit coup de pouce sur ces quelques affirmations :
*Supposons que f(x, y) est une fonction de deux variables admettant des dérivées partielles telle que pour tout (x, y) on af/;)x(x, y);)1 et
f/;)y (x, y)
0. Alors f(2, 1)
f(0, 0) + 2.
*Supposons que f(x, y) est une fonction de deux variables admettant un vecteur gradient tel que ||;););) Gradf(x, y)||1 en tout point (x, y) du plan. Alors f(1, 1)
f(0, 0) +
2.
*Soit P : RR un polynôme et soit f(x, y) = P(x^2 + y^2). Alors f(x, y) est constante sur chaque cercle de centre (0, 0) et le vecteur
;););) Gradf(2,3) est de la forme (2t, 3t) (pour un réel t convenablement choisi).
*Les solutions (x, y) de léquation (2x+y;)1)/(1+x^2y^4) = 0 sont données par y=1;)2x, xR quelconque. Donc le gradient de f(x, y) = (2x+y;)1)(1+x^2y^4) en tout point de la droite déquation y = 1;)2x est dans la direction de (;)1,2).
Qu'as-tu fait pour le moment : expose tes idées :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
fonction de deux variables
1/ 2/Je déduis des hypothèses que les applications partielles sont croissantes .
3/ Il faut voir "ce que vaut" p(x^2+y^2) sur le cercle de centre l'origine et de rayon R mais je ne comprends pas cette formulation
4/ J'ai remplace y = 1-2x dans f(x,y) et j'ai vérifie que le gradient s'annule mais je ne vois pas comment trouver sa direction?
3/ Il faut voir "ce que vaut" p(x^2+y^2) sur le cercle de centre l'origine et de rayon R mais je ne comprends pas cette formulation
4/ J'ai remplace y = 1-2x dans f(x,y) et j'ai vérifie que le gradient s'annule mais je ne vois pas comment trouver sa direction?
hello,
pour 3)
leq d'un cercle centré en (0,0) est x^2+y^2=r
ton polynome il est de la forme p(X) = somme a_n X^n, avec x réel, donc sur le cercle de rayon r, tu peux écrire
p(r) = somme a_n r^n, et en particulier, qqsoit (x,y) qui appartient au cercle de rayon r,
p(r) = p(x^2+y^2) = f(x,y)
et donc f(x,y) est constante sur le cercle de rayon r
3.2)
pour calculer le gradient, la formule est
gradf = d/dx f(x,y) e_x + d/dy f(x,y) e_y
du coup grad p(x^2+y^2) = 2x P'(r) e_x + 2y P'(r) e_y
avec P'(r) à expliciter mais j'en suis plus capable :hum:
bref tu peux factoriser par 2P'(r) et tu as donc
grandf = 2P'(r) [x,y]
et en remplacant (x,y) par (2,3) tu as le résultat
4) il doit y avoir plus fin que de calculer le gradient explicitement mais à défaut tu peux toujours calculer les dérivées partielles :mur:
pour 3)
leq d'un cercle centré en (0,0) est x^2+y^2=r
ton polynome il est de la forme p(X) = somme a_n X^n, avec x réel, donc sur le cercle de rayon r, tu peux écrire
p(r) = somme a_n r^n, et en particulier, qqsoit (x,y) qui appartient au cercle de rayon r,
p(r) = p(x^2+y^2) = f(x,y)
et donc f(x,y) est constante sur le cercle de rayon r
3.2)
pour calculer le gradient, la formule est
gradf = d/dx f(x,y) e_x + d/dy f(x,y) e_y
du coup grad p(x^2+y^2) = 2x P'(r) e_x + 2y P'(r) e_y
avec P'(r) à expliciter mais j'en suis plus capable :hum:
bref tu peux factoriser par 2P'(r) et tu as donc
grandf = 2P'(r) [x,y]
et en remplacant (x,y) par (2,3) tu as le résultat
4) il doit y avoir plus fin que de calculer le gradient explicitement mais à défaut tu peux toujours calculer les dérivées partielles :mur:
la vie est une fête 
salut
si x^2 + y^2 = r^2
alors f(x, y) = P(r^2) est constant sur le cercle de rayon r
ensuite df = 2xdP/dx + 2ydP/dy
or évidemment 2dP/dx = 2dP/dy = t car f(x, y) = f(y, x)
donc df (2, 3) = (2t, 3t)
soit d un vecteur directeur de la droite D d'équation 2x + y - 1 = 0 et n un vecteur normal
puisque f est nulle sur la droite D f(X + td) = f(X) = 0 pour tout point X de D donc grad f = kn + 0d = kn
si x^2 + y^2 = r^2
alors f(x, y) = P(r^2) est constant sur le cercle de rayon r
ensuite df = 2xdP/dx + 2ydP/dy
or évidemment 2dP/dx = 2dP/dy = t car f(x, y) = f(y, x)
donc df (2, 3) = (2t, 3t)
soit d un vecteur directeur de la droite D d'équation 2x + y - 1 = 0 et n un vecteur normal
puisque f est nulle sur la droite D f(X + td) = f(X) = 0 pour tout point X de D donc grad f = kn + 0d = kn
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Je sais pas si c'est dans un cours de math ou de physique, mais ça au niveau mathématique, on va dire poliment que c'est "bof bof" vu que le polynôme P va de R->R et qu'il ne dépend donc que d'une seule variable (et, vu le contexte, ça serait pas stupide de dire que la variable en question, ce n'est ni x ni y...)zygomatique a écrit:...ensuite df = 2xdP/dx + 2ydP/dy
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour le 1), le fait que  f/;)x(x, y);)1 pour tout x,y te dit que, quelque soit le réel y fixé, la fonction
f/;)x(x, y);)1 pour tout x,y te dit que, quelque soit le réel y fixé, la fonction ) vérifie
vérifie \geq 1) ce qui implique (théorème des valeurs intermédiaires) que,
ce qui implique (théorème des valeurs intermédiaires) que, -\varphi(x)}{x'-x}\geq 1) soit encore que
soit encore que -\varphi(x)\geq x'-x) .
.
En revenant aux notation "fonction de deux variables", cela signifie que-f(x,y)\geq x'-x) et, comme le y apparaissant dans cette formule est... quelconque, on peut même écrire que
et, comme le y apparaissant dans cette formule est... quelconque, on peut même écrire que -f(x,y)\geq x'-x) .
.
Application Numérique :-f(0,1)\geq 2-0)
De même, le fait que f/;)y (x, y)
f/;)y (x, y)  0 pour tout x,y te dit que, quelque soit le réel x fixé, la fonction
0 pour tout x,y te dit que, quelque soit le réel x fixé, la fonction ) vérifie
vérifie \geq 0) ce qui implique (théorème des valeurs intermédiaires) que,
ce qui implique (théorème des valeurs intermédiaires) que, -\psi(y)}{y'-y}\geq 0) soit encore que
soit encore que -\psi(y)\geq 0) .
.
En revenant aux notation "fonction de deux variables", cela signifie que-f(x,y)\geq 0) et, comme le x apparaissant dans cette formule est... quelconque, on peut même écrire que
et, comme le x apparaissant dans cette formule est... quelconque, on peut même écrire que -f(x,y)\geq 0) .
.
Application Numérique :-f(0,0)\geq 0)
Pour le 2) (comme pour le 1), le plus simple est de se ramener à une fonction d'une seule variable
Donc perso., je poserais bien=f(t,t)) qui est d'une seule variable et qui permet d'écrire que
qui est d'une seule variable et qui permet d'écrire que -f(0,0)|=|\varphi(1)-\varphi(0)|=(1-0)|\varphi'(c)|) pour un certain
pour un certain  (T.A.F.) reste a voir ce que l'hypothèse
(T.A.F.) reste a voir ce que l'hypothèse ||\geq 1) pour tout (x,y) signifie en ce qui concerne
pour tout (x,y) signifie en ce qui concerne )
Après, il est possible que ce que je sois en train de te suggérer là soit déjà fait dans ton cours (pour démontrer un certain théorème...) mais c'est pas forcément plus con de le refaire...
Pour le 3), vu que l'équation d'un cercle centré en O:(0,0) est (ou
(ou 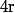 est le rayon du cercle) tout les points du cercle en question vont vérifier
est le rayon du cercle) tout les points du cercle en question vont vérifier =P(r^2)) qui est constant (sur ce cercle là)
qui est constant (sur ce cercle là)
Ensuite, les règles de dérivation d'une composée de fonctions'=v'\times u'\circ v) (pour les fonctions d'une seule variable) te disent que
(pour les fonctions d'une seule variable) te disent que =2xP'(x^2+y^2)) et que
et que =2yP'(x^2+y^2)) donc
donc =\big(4P'(13),6P'(13) \big)=(2t,3t)) si on prend
si on prend )
Pour le 4), si on veut éviter de faire trop de calcul, on écrit que où
où =2x+y-1) et
et =1+x^2y^4) (qui en fait n'intervient pas vraiment dans les calculs)
(qui en fait n'intervient pas vraiment dans les calculs)
d'où<br />=g\big( \frac{\partial h}{\partial x}\,,\,\frac{\partial h}{\partial y}\big)<br />+h\big(\frac{\partial g}{\partial x}\,,\,\frac{\partial g}{\partial y}\big))
Et, lorsque l'on calcule le gradient en un point (x,y) tel que=0) on obtient
on obtient ) qui est colinéaire au vecteur
qui est colinéaire au vecteur =(2,1))
En revenant aux notation "fonction de deux variables", cela signifie que
Application Numérique :
De même, le fait que
En revenant aux notation "fonction de deux variables", cela signifie que
Application Numérique :
Pour le 2) (comme pour le 1), le plus simple est de se ramener à une fonction d'une seule variable
Donc perso., je poserais bien
Après, il est possible que ce que je sois en train de te suggérer là soit déjà fait dans ton cours (pour démontrer un certain théorème...) mais c'est pas forcément plus con de le refaire...
Pour le 3), vu que l'équation d'un cercle centré en O:(0,0) est
Ensuite, les règles de dérivation d'une composée de fonctions
Pour le 4), si on veut éviter de faire trop de calcul, on écrit que
d'où
Et, lorsque l'on calcule le gradient en un point (x,y) tel que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Parce que... c'est ce qu'il y a d'écrit dans ton énoncé... :marteau:
Par contre, effectivement, je ne comprend pas franchement ce que le "donc" vient faire dans la phrase : je me contente donc de montrer que ce qu'il y a derrière le "donc" en question est effectivement vrai sans tenir compte de la phrase précédente (vu que je ne vois pas franchement le lien entre ce qu'il y avant et ce qu'il y a après le fameux "donc")
yanisdourge a écrit:...le gradient de f(x, y) = (2x+y;)1)(1+x^2y^4) ...
Par contre, effectivement, je ne comprend pas franchement ce que le "donc" vient faire dans la phrase : je me contente donc de montrer que ce qu'il y a derrière le "donc" en question est effectivement vrai sans tenir compte de la phrase précédente (vu que je ne vois pas franchement le lien entre ce qu'il y avant et ce qu'il y a après le fameux "donc")
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
