bonjour
Je dois trouver l'eventuel limite en (0,0) de f(x,y)=xy^2/(x^2+y^4).
Je pense que c'est 0 mais j'arrive pas à prouver.
Merci
Fonction de 2 var
34 messages
- Page 1 sur 2 - 1, 2
par nekros » 21 Juil 2006, 13:39
Salut,
Je n'ai qu'abordé les fonctions de deux variables, donc c'est juste une idée :
On a=\frac{xy^2}{x^2+y^4})
On a=0--->0)
quand 
tend vers 
On a=0--->0)
quand 
tend vers
On pose=0)
Ensuite, il faut montrer que-f(0,0)| \le g(N))
où  =0)
et )
(
est une norme)
Au fait, au démoninateur, c'est bien
?
Thomas G :zen:
Je n'ai qu'abordé les fonctions de deux variables, donc c'est juste une idée :
On a
On a
On a
On pose
Ensuite, il faut montrer que
Au fait, au démoninateur, c'est bien
Thomas G :zen:
par kms040584 » 21 Juil 2006, 14:26
Salut,
non, il ne suffit pas de faire tendre x et y séparement vers 0 pour trouver la limite, mais il faut faire tendre le couple (x,y) vers (0,0).
Ici, je pense qu'en utilisant différents chemins, on peut prouver qu'elle n'existe pas.
Par exemple en prenant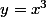
, qui est bien continue, qui tend vers 0 quand x->0, etc...
tu as :=x^7 / (x^2+x^12))
qui n'a pas de limite finie en (0,0)
et en prenant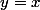
, tu as =x^3/(x^2+x^4))
qui tend vers 0.
Or si il y avait une limite en (0,0), elle serait la même quelque soit le "chemin d'approche."
Donc y'a pas de limite.
K.
non, il ne suffit pas de faire tendre x et y séparement vers 0 pour trouver la limite, mais il faut faire tendre le couple (x,y) vers (0,0).
Ici, je pense qu'en utilisant différents chemins, on peut prouver qu'elle n'existe pas.
Par exemple en prenant
tu as :
et en prenant
Or si il y avait une limite en (0,0), elle serait la même quelque soit le "chemin d'approche."
Donc y'a pas de limite.
K.
par alben » 21 Juil 2006, 14:30
Bonjour,
Je ne pense pas que ça puisse marcher, il suffit de prendre pour tout y petit un x égal à ky² qui sera également très petit. Pourtant f(x,y) sera égal à k/(1+k²) clairement différent de zéro.
Par exemple avec k=1, on trouve f(x,y)>=0,5
Plus rigoureusement, ce raisonnement doit te permettre de démontrer que la fonction n'a pas de limite en (0,0)
ps :télescopage !
Je ne pense pas que ça puisse marcher, il suffit de prendre pour tout y petit un x égal à ky² qui sera également très petit. Pourtant f(x,y) sera égal à k/(1+k²) clairement différent de zéro.
Par exemple avec k=1, on trouve f(x,y)>=0,5
Plus rigoureusement, ce raisonnement doit te permettre de démontrer que la fonction n'a pas de limite en (0,0)
ps :télescopage !
par dilzydils » 21 Juil 2006, 14:37
kms040584: f(x,x^3) tend vers 0: factorise par x^2.
alben: je doute que ton truc soiit juste, d'ailleurs j'arrive à prouver que f(x,y)<=1/2 car (x-y^2)^2=x^2+y^4-2xy^2>=0
alben: je doute que ton truc soiit juste, d'ailleurs j'arrive à prouver que f(x,y)<=1/2 car (x-y^2)^2=x^2+y^4-2xy^2>=0
par nekros » 21 Juil 2006, 14:41
kms040584 a écrit:Salut,
non, il ne suffit pas de faire tendre x et y séparement vers 0 pour trouver la limite, mais il faut faire tendre le couple (x,y) vers (0,0).
Ici, je pense qu'en utilisant différents chemins, on peut prouver qu'elle n'existe pas.
Par exemple en prenant
tu as :
et en prenant
Or si il y avait une limite en (0,0), elle serait la même quelque soit le "chemin d'approche."
Donc y'a pas de limite.
K.
Salut kms040584,
Le quotient tend vers 0 quand x tend vers 0.
Thomas G :zen:
par nekros » 21 Juil 2006, 14:45
Pourquoi ne pas utiliser une caractérisation séquentielle, ou déterminer la limite de )
quand 
tend vers ?
On trouve que = 0=f(0,0)})
.
Donc
est bien continue en )
, non ?
Thomas G :zen:
On trouve que
Donc
Thomas G :zen:
par kms040584 » 21 Juil 2006, 14:55
euh, pour le calcul de f(x,x^3), je vois pas trop comment tu obtiens ca...
ensuite excuse pour la limite... j'abuse un peu beaucoup! on va dire que c'est vendredi:marteau:
en revanche en prenant
on a:
=x^2/(x^2+x^2)=1/2)
non?
ensuite excuse pour la limite... j'abuse un peu beaucoup! on va dire que c'est vendredi:marteau:
en revanche en prenant
on a:
par dilzydils » 21 Juil 2006, 14:55
nekros, je crois pas que ton truc marche parcke tes 2 variables sont liées alors qu'elles peuvent varier indépendemment l'1 de l'autre...
par aviateurpilot » 21 Juil 2006, 14:55
je ne connais pas les fonctions avec 2 variable
mais je pense que si f a la meme limite que
c'est 0.
par nekros » 21 Juil 2006, 14:57
kms, désolé pour le calcul, t'as raison, on va dire que c'est la chaleur :ptdr:
Thomas G :zen:
Thomas G :zen:
par kms040584 » 21 Juil 2006, 15:01
lol, oui!
en revanche, quant a mon raisonnement, c'est très souvent comme cela qu'on prouve qu'une fonction n'a pas de limite. On cherche deux fonctions y=f1(x) et y=f2(x) avec les limites de f1 et f2 égale à 0 en 0 (dans ce cas), tel que f(x,f1(x)) et f(x,f2(x)) n'ont pas la meme limite. En revanche, la reciproque est fausse. Trouver une limite à f(x,f1(x)) ne signifie pas que la fonction f(x,y) à une limite en (0,0). C'est pour cela que ton f(h,th) n'est pas suffisant.
en revanche, quant a mon raisonnement, c'est très souvent comme cela qu'on prouve qu'une fonction n'a pas de limite. On cherche deux fonctions y=f1(x) et y=f2(x) avec les limites de f1 et f2 égale à 0 en 0 (dans ce cas), tel que f(x,f1(x)) et f(x,f2(x)) n'ont pas la meme limite. En revanche, la reciproque est fausse. Trouver une limite à f(x,f1(x)) ne signifie pas que la fonction f(x,y) à une limite en (0,0). C'est pour cela que ton f(h,th) n'est pas suffisant.
par nekros » 21 Juil 2006, 15:12
Ok,
Tu sais j'en ai pas fait souvent.
Pour compléter ma méthode, on peut aussi utiliser une caractérisation séquentielle...
Mais n'oublions pas que : Ce n'est qu'en essayant continuellement, que l'on finit par réussir
Ou, en d'autres termes : plus ça rate, plus on a de chance que ça marche....
Thomas G :zen:
Tu sais j'en ai pas fait souvent.
Pour compléter ma méthode, on peut aussi utiliser une caractérisation séquentielle...
Mais n'oublions pas que : Ce n'est qu'en essayant continuellement, que l'on finit par réussir
Ou, en d'autres termes : plus ça rate, plus on a de chance que ça marche....
Thomas G :zen:
par aviateurpilot » 21 Juil 2006, 15:25
f (definie sur R² ) a le meme comportement de g (definie sur 
)
avec=\frac{xy}{x^2+y^2})
avec
par nekros » 21 Juil 2006, 15:37
Si c'est le cas, je vais essayé de me faire la main...
On considère=\frac{xy}{x^2+y^2})
Les applications partielles)
et )
sont nulles donc continues.
Or,=\frac{1}{2})
pour tout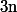 
dans 
On a donc=\frac{1}{2} \neq f(0,0))
Ceci contredit donc la caractérisation séquentielle de la continuité et donc
n'est pas continue en
Donc pas de limite en
Quelqu'un peut-il confirmer (ou infirmer)
Thomas G :zen:
On considère
Les applications partielles
Or,
On a donc
Ceci contredit donc la caractérisation séquentielle de la continuité et donc
Donc pas de limite en
Quelqu'un peut-il confirmer (ou infirmer)
Thomas G :zen:
par nekros » 21 Juil 2006, 15:43
Arf oui,
Si l'énoncé proposait : est-ce qu'on a f(0,0)=0 ?
Là ça aurait été correct, et ça devient un raisonemment par l'absurde en supposant que f(0,0)=0
Thomas G :zen:
Si l'énoncé proposait : est-ce qu'on a f(0,0)=0 ?
Là ça aurait été correct, et ça devient un raisonemment par l'absurde en supposant que f(0,0)=0
Thomas G :zen:
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :