Fonction de 2 var definie par integrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 17 Sep 2015, 14:23
par adamNIDO » 17 Sep 2015, 14:23
Bonjour,
s'il vous plait une indication ou un lien de cours pour resoudre cette question

merci
-
mathelot
 par mathelot » 17 Sep 2015, 14:47
par mathelot » 17 Sep 2015, 14:47
adamNIDO a écrit:Bonjour,
s'il vous plait une indication ou un lien de cours pour resoudre cette question

merci
si on suppose f continue, introduire une primitive F de f pour écrire l'intégrale.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 17 Sep 2015, 15:03
par adamNIDO » 17 Sep 2015, 15:03
mathelot a écrit:si on suppose f continue, introduire une primitive F de f pour écrire l'intégrale.
j'ai aucune information concernant la régularité de

donc comme tu as dit on suppose que

continue sur intervalle
, v(x,y)])
alors elle admet une primitive on la note par

=\int_{u(x,y)}^{v(x,y)}f(s)\textrm{d}s=F(u(x,y))-F(v(x,y))
alors sa différentielle vaut
=\int_{u(x,y)}^{v(x,y)}f(s)\textrm{d}s=u'(x,y)F'(u(x,y))-v'(x,y)F'(v(x,y))
-
mathelot
 par mathelot » 17 Sep 2015, 15:13
par mathelot » 17 Sep 2015, 15:13
adamNIDO a écrit:j'ai aucune information concernant la régularité de

donc comme tu as dit on suppose que

continue sur intervalle
, v(x,y)])
alors elle admet une primitive on la note par

=\int_{u(x,y)}^{v(x,y)}f(s)\textrm{d}s=F(u(x,y))-F(v(x,y))
alors sa différentielle vaut
=\int_{u(x,y)}^{v(x,y)}f(s)\textrm{d}s=u'(x,y)F'(u(x,y))-v'(x,y)F'(v(x,y))
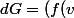 \frac{\partial v}{\partial x}-f(u) \frac{\partial u}{\partial x})dx+(f(v) \frac{\partial v}{\partial y}-f(u) \frac{\partial u}{\partial y})dy)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 17 Sep 2015, 15:27
par adamNIDO » 17 Sep 2015, 15:27
mathelot a écrit: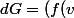 \frac{\partial v}{\partial x}-f(u) \frac{\partial u}{\partial x})dx+(f(v) \frac{\partial v}{\partial y}-f(u) \frac{\partial u}{\partial y})dy)
=\int_{u(x,y)}^{v(x,y)}f(s)\textrm{d}s=F(u(x,y))-F(v(x,y))\\<br /><br />G(x,y)=\int_{u(x,y)}^{v(x,y)}f(s)\textrm{d}s<br />G(x,y)=\int_{u(x,y)}^{0}f(s)\textrm{d}s+\int_{0}^{v(x,y)}f(s)\textrm{d}s \\<br />G(x,y)=\int_{0}^{v(x,y)}f(s)\textrm{d}s -\int_{0}^{u(x,y)}f(s)\textrm{d}s \\)
alors
=(f(v))' -(f(u))' \\<br />G'(x,y)=v'f(v) -u'f(u) \\<br />G'(x,y)=(\frac{\partial v}{\partial x}dx+\frac{\partial v}{\partial y}dy ) f(v) -(\frac{\partial v}{\partial x}dx+\frac{\partial v}{\partial y}dy ) f(u) \\<br />dG=(f(v) \frac{\partial v}{\partial x}-f(u) \frac{\partial u}{\partial x})dx+(f(v) \frac{\partial v}{\partial y}-f(u) \frac{\partial u}{\partial y})dy)
Est ce que c'est ca la méthode de plus si possible de m'explique pourquoi pas on utilise pas la fonction F pour avoir l'expression de la différentiabilité de G
merci d'avance
-
mathelot
 par mathelot » 17 Sep 2015, 15:47
par mathelot » 17 Sep 2015, 15:47
adamNIDO) a écrit:Est ce que c'est ca la méthode de plus si possible de m'explique pourquoi pas on utilise pas la fonction F pour avoir l'expression de la différentiabilité de G
merci d'avance
on l'utilise . f(v)=F'(v)
-
Robot
 par Robot » 17 Sep 2015, 15:51
par Robot » 17 Sep 2015, 15:51
adamNIDO a écrit:=\int_{u(x,y)}^{v(x,y)}f(s)\textrm{d}s=F(u(x,y))-F(v(x,y)))
Tu es vraiment sûr que si

est une primitive de

, alors
\,ds=F(u)-F(v))
?
Par ailleurs tu écris
)
. Quel sens cela a-t-il pour une fonction de deux variables ?
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 17 Sep 2015, 16:02
par adamNIDO » 17 Sep 2015, 16:02
Robot a écrit:Tu es vraiment sûr que si

est une primitive de

, alors
\,ds=F(u)-F(v))
?
Par ailleurs tu écris
)
. Quel sens cela a-t-il pour une fonction de deux variables ?
c'etait faute de frappe, je veux dire
\,ds=F(v)-F(u))
la différentiabilité de G sera les dérivée partielle par rapport x et y
-
Robot
 par Robot » 17 Sep 2015, 16:06
par Robot » 17 Sep 2015, 16:06
adamNIDO a écrit:la différentiabilité de G sera les dérivée partielle par rapport x et y
Je ne comprends pas le sens de cette phrase. Peux-tu l'expliquer ?
Tu écris
)
. Je te demande : qu'est-ce que la dérivée d'une fonction de deux variables ? Qu'est-ce que ce
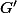
?
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 17 Sep 2015, 16:18
par adamNIDO » 17 Sep 2015, 16:18
Robot a écrit:Je ne comprends pas le sens de cette phrase. Peux-tu l'expliquer ?
Tu écris
)
. Je te demande : qu'est-ce que la dérivée d'une fonction de deux variables ? Qu'est-ce que ce
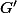
?
si je me rappel bien sera
=\frac{\partial G}{\partial x}(x,y)dx+\frac{\partial G}{\partial y}(x,y)dy)
-
mathelot
 par mathelot » 17 Sep 2015, 18:00
par mathelot » 17 Sep 2015, 18:00
adamNIDO a écrit:si je me rappel bien sera
=\frac{\partial G}{\partial x}(x,y)dx+\frac{\partial G}{\partial y}(x,y)dy)
=\frac{\partial G}{\partial x}(x,y)dx+\frac{\partial G}{\partial y}(x,y)dy)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 17 Sep 2015, 18:06
par adamNIDO » 17 Sep 2015, 18:06
Soit

est continue et

sont de classe
 Question :
Question : 
est elle bien définie :
f est continue donc f est bien définie

est elle continue :

est elle differentiable :
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités

