Fonction Usuelle

par **Fast78** » 21 Oct 2012, 16:51

Soit f(x)= arcsin(2x/1+x^2) et Y(t)= arcsin(sin(t))
Voici la question: Montrer que our tout x appartenant ]-Pi/2,Pi/2[, f(tant)=Y(t)
J'ai essayé pleins de choses mais je ne tombe jamais sur Y(t) Pouvez vous m'aidez svp?

par **cuati** » 21 Oct 2012, 17:10

Fast78 a écrit:Soit f(x)= arcsin(2x/1+x^2) et Y(t)= arcsin(sin(t))
Voici la question: Montrer que our tout x appartenant ]-Pi/2,Pi/2[, f(tant)=Y(t)
J'ai essayé pleins de choses mais je ne tombe jamais sur Y(t) Pouvez vous m'aidez svp?

Ça me parait faux avec

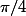
... ce serait pas plutôt

par **Fast78** » 21 Oct 2012, 17:14

J'ai bien recopié la question sinon donner moi une adresse de messagerie je vous enverrais lénoncé en PDF.

par **Manny06** » 21 Oct 2012, 17:22

Fast78 a écrit:J'ai bien recopié la question sinon donner moi une adresse de messagerie je vous enverrais lénoncé en PDF.

sur un autre site on trouve le même exercice mais avec arcsin(sin(2t))

par **cuati** » 21 Oct 2012, 17:23

Fast78 a écrit:....Montrer que our tout x appartenant ]-Pi/2,Pi/2[, f(tant)=Y(t)...

C'est x ou t ? ou il y a une relation implicite entre x et t ?

par **cuati** » 21 Oct 2012, 17:24

Manny06 a écrit:sur un autre site on trouve le même exercice mais avec arcsin(sin(2t))

Ouais c'est bien ce qu'il me semblait.... :triste:

par **Fast78** » 21 Oct 2012, 17:27

Ah mince désolé c'est bien arcsin(sin(2t))

par **Fast78** » 21 Oct 2012, 17:29

Voici lénoncé sans fautes cette fois:
Soit f(x)= arcsin(2x/1+x^2) et Y(t)= arcsin(sin(2t))
Voici la question: Montrer que pour tout t appartenant ]-Pi/2,Pi/2[, f(tant)=Y(t)

par **Manny06** » 21 Oct 2012, 17:41

Fast78 a écrit:Voici lénoncé sans fautes cette fois:
Soit f(x)= arcsin(2x/1+x^2) et Y(t)= arcsin(sin(2t))
Voici la question: Montrer que pour tout t appartenant ]-Pi/2,Pi/2[, f(tant)=Y(t)

pose x=tant dans la formule 2x/(1+x²)

par **Fast78** » 21 Oct 2012, 18:05

C'est ce que j'ai fait mais je ne tombe pas sur Y(t)

Fonction Usuelle

Fonction Usuelle

Qui est en ligne