Fonction périodique

[Mohamed]

salut les amis
j'ai un petit problème avec un exercice, veuillez m'aider à faire,

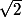
Mq 'une fonction continue et périodique dont 1 et sont des périodes est constante.........

HM

[fahr451]

l 'ensemble H des périodesde f est un sous groupe de (R,+)
avec la définition T un réel est une période de f si pour tout x :f(x+T)= f (x)
0 est donc une période
1 et sqrt(2) étant deux périodes: G = Z + sqrt(2) Z est inclus ds H
or un sous groupe de R est soit aZ soit dense ds R comme sqrt(2) n 'est pas rationnel G est forcément d e la deuxième forme donc dense ds R et H aussi
on en déduit par continuité de f que f est constante

REM on parlera de "la" période d'une fonction périodique ds le cas où H est non réduit à {0} et de la forme aZ La période sera alors a ( a >0)