j'aurais besoin d'aide pour un exo:
On définit sur R pour tout t>0
Soit
(Mg c'est la fonction maximale de Hardy-Littlewood de g)
Merci !
Fonction maximale
3 messages
- Page 1 sur 1
fonction maximale
par infernaleur » 01 Oct 2020, 14:20
Bonjour !
j'aurais besoin d'aide pour un exo:
On définit sur R pour tout t>0
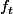
par =\frac{1}{\sqrt{4 \pi t}}e^{-\frac{x^2}{4t}})
Soit)
, montrer que (x)| \leq (Mg)(x))
pour tout t>0 et x réel.
(Mg c'est la fonction maximale de Hardy-Littlewood de g)
Merci !
j'aurais besoin d'aide pour un exo:
On définit sur R pour tout t>0
Soit
(Mg c'est la fonction maximale de Hardy-Littlewood de g)
Merci !
Re: fonction maximale
par Ben314 » 02 Oct 2020, 17:01
Salut,
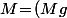Vu la définition de(x))
on a clairement intérêt à poser \!=\!\int_{x-v}^{x+v}\!\!|g(u)|\,du)
(avec 
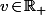
) de façon à avoir \!\leq\!2Mv)
pour tout 
.
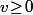
Le but étant ensuite de "faire apparaître" cette fonction
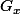
dans le terme de gauche :
(x)| =\left|\int_{-\infty}^{+\infty}\!g(u)f_t(x\!-\!u)\,du\right|\leq\int_{-\infty}^{+\infty}\!|g(u)|f_t(x\!-\!u)\,du=\int_{-\infty}^{+\infty}\!|g(u)|\Bigg(\int_{|x-u|}^{+\infty}\!\!(-f_t')(v)\,dv\!\Bigg)du)
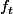
en utilisant la parité de. Ensuite, vu que tout est positif là dedans, on peut utiliser Fubini ce qui donne
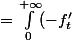(v)\Bigg(\int_{x-v}^{x+v}|g(u)|\,du\!\Bigg)dv=\int_0^{+\infty}\!(-f_t')(v)G_x(v)dv)
La majoration de)
puis le bête calcul de (v)dv)
permet alors de conclure.
Vu la définition de
Le but étant ensuite de "faire apparaître" cette fonction
en utilisant la parité de
La majoration de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: fonction maximale
par infernaleur » 02 Oct 2020, 17:19
Merci pour l'aide !
Et bon retour à toi dans le forum ça fait plaisir de te revoir.
Et bon retour à toi dans le forum ça fait plaisir de te revoir.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 111 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :