Fonction intégrable?

par **Clarissa** » 21 Juin 2006, 18:48

Rebonjour!
je ne comprends pas pourquoi la fonction complexe 1/z est intégrable sur le disque unité complexe. Je n'ai pas plus de détail dans mon corrigé.
N'y a-t-il pas un problème en 0?
Merci de m'aider.

par **tize** » 21 Juin 2006, 19:13

Bonjour,
en quelle classe es-tu ?
es-tu sur que c'est le disque et pas le cercle unité ?
cordialement

par **yos** » 21 Juin 2006, 19:22

Oui, c'est sur le cercle.

.
Ou encore

et le résidu est 1.

par **Clarissa** » 21 Juin 2006, 19:34

c'est ce que je me suis dit aussi pour le coup du disque, mais j'ai bien relu l'énoncé et c'est bien noté le disque unité du plan complexe. En fait on me dit que g est une fonction bornée sur ce disque et aprés avoir montré que 1/z est intégrable sur le disque cela me permet de conclure que g(z)/z appartient à L^1(disque unité).
Sinon je suis en master 1 de math mais en difficulté :-)

par **yos** » 21 Juin 2006, 20:07

Alors je ne sais pas! Ton énoncé me semble bizarre mais comme mes restes en analyse complexe sont lacunaires, je préfère ne pas t'égarer davantage.

par **El_Gato** » 23 Juin 2006, 12:03

Il est vraiment bizarre cet enoncé, car si ce n'est pas d'intégration sur un cercle dont on parle, alors il ne peut s'agir que d'intégration de la fonction

considérée comme une fonction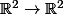

, autrement dit la fonction:

.

Mais alors, quand on parle d'espace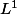

on fait référence à l'intégrabilité du module. Donc ici on ferait référence à l'intégrabilité de

qui doit ressortir de celle de

(jacobien qui doit être de l'ordre de r je crois) c'est cela ?

Si c'est cela c'est exotique comme exo.

par **nox** » 23 Juin 2006, 12:19

On peut montrer qu'elle est intégrable presque partout sur le disque unité. Et la fonction est de Z dans Z : on parle de disque dans le plan complexe j'imagine.

par **nox** » 23 Juin 2006, 12:29

La fonction est de Z dans Z on parle de disque complexe j'imagine.

Disque privé de son centre pour moi c'est une erreur d'énoncé...

par **El_Gato** » 23 Juin 2006, 14:24

nox a écrit:La fonction est de Z dans Z on parle de disque complexe

De

dans

tu veux dire.

par **nox** » 23 Juin 2006, 14:27

euh oui :ptdr:

merci :)

Fonction intégrable?

Fonction intégrable?

Qui est en ligne