Lierre Aeripz a écrit:Voici une solution correcte :
Soit
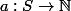
une bijection.
Une solution du problème proposé est alors donnée par
 = \sum_{y \leq x} 2^{-a(y)})
. Comme S est dénombrable et que
_n)
est une famille sommable, la somme est toujours finie. Comme les termes sont strictement positifs, la croissance stricte est triviale.
excusez moi mais je n'ai absolument pas compris :$
sinon aviateurpilot la puissance d'un ensemble est équivalente a son cardinal, c'est juste une autre appellation.
Cependant, j'ai un problème, d'après wikipedia "Un ensemble infini est dit dénombrable si, et seulement si, il existe une bijection entre lui et

. Intuitivement, un ensemble infini est dénombrable si, et seulement si, on peut « énumérer » ses éléments: le « premier » élément, le « deuxième » élément, le « troisième » élément, et ainsi de suite sans s'arrêter."
Ainsi, donc d'après la définition d'un ensemble dénombrable, il existe directement une bijection? Est ce ça ou est ce que je me trompe ? Je vois pas ou est la subtilité pour des ensembles ayant des cardinaux transfinis...
bien ordonné, dénombrable, mais l'ensemble des éléments strictement inférieurs à
est infini...
