Fonction de V.A. & Image réciproque
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Evanou
- Messages: 9
- Enregistré le: 22 Fév 2020, 17:56
-
 par Evanou » 22 Fév 2020, 18:52
par Evanou » 22 Fév 2020, 18:52
Bonjour, Bonsoir,
Je bloque sur un détail d'analyse de L2 au détour d'un exercice de probas. Je m'explique: il m'est demandé de calculer la densité d'une fonction de variables aléatoires, et, dans le théorème que je veux utiliser, il est question d'image réciproque qui me fait grincer des dents ! Voici l'énoncé de l'éxo:
Soit

va de densité
=1_{0<u<1}(u)2u)
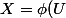=U(1-U))
, Calculer

.
Je sais que sous certaines conditions sur

, comme

et bijective au moins par parties (sur union finie d'intervales disjoints), on a:
}(u)=\sum\limits_{\substack{y \in E, \phi(x)=y, \phi'(x) \neq 0}} f_{X}(x) \frac{1}{<br />\vert \phi'(y )\vert })
Ducoup je dois calculer
)
, facile pour
=x^2)
par exemple, on a
 = { \sqrt{x}, -\sqrt{x}, 0})
mais pour
=x - x^2)
.... je bloque completement, une idée pour m'aider ?
En espérant avoir été clair

Merci beaucoup !

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Fév 2020, 18:58
par Lostounet » 22 Fév 2020, 18:58
Salut,
Pour trouver la fonction réciproque de y(x)=x^2 on cherche à partir de l'image y et trouver une fonction g telle que g(y)=x.
Toute précaution prise etc, cela revient à résoudre
y=x^2 pour trouver x(y)= +- sqrt(y) grosso modo.
Donc pour ta fonction, il faut résoudre x^2-x=y en considérant y connu.
C'est une équation du second degré x^2-x-y=0 où l'on sait exprimer les solutions avec delta sous réserve d'existence. Ces solutions sont fonction de y.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Evanou
- Messages: 9
- Enregistré le: 22 Fév 2020, 17:56
-
 par Evanou » 22 Fév 2020, 19:19
par Evanou » 22 Fév 2020, 19:19
Merci beaucoup pour votre réponse rapide ! (et claire !)
Ducoup si je suis bien ma formule sans m'emmêler les pinceaux, je me retrouve avec :
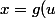 = \phi ^{-1}(u) = \lbrace \frac{1 + \sqrt{1+4u} }{2} ; \frac{1 - \sqrt{1+4u} }{2} \rbrace)
=f_{\phi(U)}(g(u))=f_{U}(\frac{1 + \sqrt{1+4u} }{2}) \frac{1}{\vert -\sqrt{1+4u} \vert} + f_{U}(\frac{1-\sqrt{1+4u}}{2})\frac{1}{\vert \sqrt{1+4u} \vert})
Sans tenir compte des possibles erreurs de calculs et/ou mixages de variables, est ce que ça semble cohérent ?
Si oui, je pense avoir compris! Merci encore

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités

