La réponse de Shadok est évidemment plus directe ; comme vous étiez parti sur l'absurde j'étais resté sur ce terrain.
Si vous supposez que
\neq f(0))
, alors
\neq f(0))
f est continue en 0 donc vous pouvez passez à la limite
=f(0))
puisque la fonction
)
est constante.
Mais par continuité en zéro,
=f(\lim_{\lambda\rightarrow 0}(\lambda x_0))=f(0)))
d'où la contradiction.
Si vous voulez vraiment "vérifier" cela avec les epsilon, prenez
-f(0)|}{2})
, vous aurez donc (par définition de la continuité) l'existence de
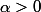
tel que
-f(0)|<\varepsilon)
Mais alors en prenant lambda tel que
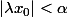
(par exemple,
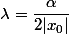
) vous avez votre contradiction.
Evidemment, ce dernier développement n'est pas nécessaire, mais je le trouve pédagogique pour bien comprendre ce que signifie la formule "pour tout epsilon, il existe alpha...", ainsi que la compréhension de l'écart entre f(0) et f(x) quand x tend vers 0 (mécanisme utilisé dans plusieurs démonstrations de théorème) . Une fois qu'on a bien compris comment tout cela fonctionne, le principe de "passer la limite dans la fonction" quand f est continue est bien plus que suffisant et élégant.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
