Rebonjour Dreck,
Je ne sais pas si tu as retrouvé la définition de ta fonction... ^^'
Pour ce qui est d'une définition à partir de l'exponentielle, la seule chose que je peux te proposer en plus de la définition à partir d'une limite que j'ai mise plus haut c'est la vraie définition de
)
comme intégrale de la fonction de Dirac
)
.
=\frac {1} {\varepsilon\sqrt{\pi}}e^{-\frac {x^2}{\varepsilon^2}})
lorsque

Comme
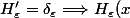=\int_{-\infty}^x \delta_\varepsilon(t)dt=\frac {1} {\varepsilon\sqrt{\pi}}\int_{-\infty}^x e^{-\frac {t^2}{\varepsilon^2}}dt)
Après, peut-être que tu peux trouver quelque chose au niveau des transformations de Laplace ou autres, mais c'est au-delà de mes compétences, je suis désolé...
Très sincèrement, je pense que la meilleure définition possible de

(pour ici en tout cas) est
))
et si tu peux poser comme cas
=\frac {1}{2})
, c'est le must car c'est ce que tu trouves pour la définition à partir de l'intégrale. :lol3:
