Fonction/dérivées/équations polynomiales

[Norma]

J'en suis donc à calculer les limites, est-ce juste ?

je cherche



car



car=

donc

la première limite est fausse

compare avec la deuxième ... dans laquelle on ne développera surtout pas (car on pourrait faire apparaitre une forme indéterminée (ce qui est le cas en -oo mais pas en +oo)

[laetidom]

à la calculatrice : ---->

graphiquement :

[Norma]

Et donc pour le même calcul avec

Je trouve

Pour f(x)

[laetidom]

Et donc pour le même calcul avec

Je trouve

Pour f(x)

Vers quoi tend f(x) quand x tends vers . . . ? :

graphique :



calcul :

en l'infini, la méthode est de factoriser au numérateur et au dénominateur par le terme de plus haut degré :

====> x² se simplifie et donc f(x) tend vers . . .(lorsque x --> )

[Norma]

Bon je reprends,

je cherche



car



car

donc

= ????

[laetidom]

De plus, si ta courbe tendait vers lorsque x tend vers on aurait quelque chose comme la courbe alors que nous avons la courbe :

[Norma]

1 ?

Ce qui permet de dire que dans tous les cas f(x) sera bien positive

[laetidom]

1 ?

On reprend, sur quel point PRECIS ça coince . . . ?

[laetidom]

1 ?

Ce qui permet de dire que dans tous les cas f(x) sera bien positive

La lim est = 1, ok super !

Ca à rien à voir avec le fait que oui, effectivement, Cf est >=0 sur le Df . . .


Et si on veut préciser les choses, on s'aperçoit sur le graphe que la courbe vient " tendre vers" l'horizontale d'équation y = 1 en arrivant par dessous, donc la limite est

[Norma]

En fait je pense commencer à "à peu prêt" tenir le principe de "x tend vers" pour calculer les limites.

Mais lorsqu'il s'agit de remplacer les limites dans la formule je coince bêtement; -+- tout ça ça va, mais 0- et 0+ je ne me les représente pas

"Ca à rien à voir avec le fait que oui, effectivement, Cf est >=0 sur le Df . . ."

Ca ne veut pas dire ducoup qu'avec les limites calculées en fonction de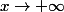 et on peut déduire que la courbe sera positive pour toute valeur de x ?

[laetidom]

Les limites servent pour déterminer les asymptotes et aussi à compléter le tableau de variations de la fonction pour être capable, à main levée, de dessiner en quelques secondes l'allure de Cf . . .

[Norma]

justement, les questions d'après concernent la dérivée le tableau de variation, la représentation graphique et la tengente.

a) calculer f'(x). Vérifier que le signe de f'(x) est celui de -x²+2x
b) Déterminer les variations de la fonction f avec le tableau de variation
c)Déterminer une équation de la tangente T1 à la courbe C au point d'abscisse 0 et une équation de la tangente T2 à C au point d'abscisse 4.
d) Représenter graphiquement T1, T2 et C.

Je vais me plonger dedans et essayer de le faire avec les "cours" que j'ai.


De plus : Faut-il représenter dans le graphique l'asymptote.. et ... à quoi ça sert ???

[laetidom]

justement, les questions d'après concernent la dérivée le tableau de variation, la représentation graphique et la tengeante.

a) calculer f'(x). Vérifier que le signe de f'(x) est celui de -x²+2x
b) Déterminer les variations de la fonction f avec le tableau de variation
c)Déterminer une équation de la tangente T1 à la courbe C au point d'abscisse 0 et une équation de la tangente T2 à C au point d'abscisse 4.
d) Représenter graphiquement T1, T2 et C.

Je vais me plonger dedans et essayer de le faire avec les "cours" que j'ai.

On arrive dans " le lourd " (non, j'exagère ! - sourire -), sais-tu dériver ? i-e déterminer la pente de la tangente à Cf sur le Df ?


Df : Domaine de Définition

[laetidom]

De plus : Faut-il représenter dans le graphique l'asymptote.. et ... à quoi ça sert ???

Oui, bien sûr ! dsl je l'ai oublié juste avant . . .

Ca sert à être complet !, à voir le comportement de la courbe donc de la fonction, apercevoir les " tendre vers . . ." et les valeurs interdites du Df . . .

[Norma]

Je vais essayer, je me demande simplement si je dois dériver f(x) de l'énoncé initial (x²/(x-1)²) ou ou f(x) avec a,b,c qu'on a déterminés plus tôt. Est-ce que le résultat sera le même ?

Je vais tenter et je reviendrais poster à la suite ici pour voir si je tiens le bon bout . En tout cas... merci beaucoup! Sans toi/vous je ne m'en sortirai pas et j'en serais encore à essayer de comprendre le pseudo cours sur les fonction que j'ai...

[laetidom]

Ok, moi aussi il faut que je m'absente, donc @+ sans problème et bon courage ! :

Je vais essayer, je me demande simplement si je dois dériver f(x) de l'énoncé initial (x²/(x-1)²) ou ou f(x) avec a,b,c qu'on a déterminés plus tôt. Est-ce que le résultat sera le même ?

Prendre la version qui te semble la plus aisée, faire les 2 te permettra de t'exercer, et oui heureusement que l'on trouve le même résultat !

Je vais tenter et je reviendrais poster à la suite ici pour voir si je tiens le bon bout . En tout cas... merci beaucoup! Sans toi/vous je ne m'en sortirai pas et j'en serais encore à essayer de comprendre le pseudo cours sur les fonction que j'ai...

On est tous passés par là !, seulement nous on l'a déjà intégré ! et passé le cap on kiff ! . . .

[Norma]

Effectivement je n'en suis pas encore à kiffer moi....

Bon j'ai déjà un problème sur la dérivée... Je cherche la dérivée de

Et je trouve

Et pour

Je trouve également f'(x)=-2

[laetidom]

Effectivement je n'en suis pas encore à kiffer moi....

J'imagine bien ! . . .

Bon j'ai déjà un problème sur la dérivée... Je cherche la dérivée de

Et je trouve

Et pour

Je trouve également f'(x)=-2

En fait,

Donc,


et

Je te laisse décortiquer . . .

[laetidom]

Petit complément :

Tu avais trouvé f ' (x) = -2

N'oublions pas que f ' (x) représente la valeur de la tangente à Cf en tout point du Df, donc avec ta valeur, crois-tu que la pente de la tangente soit toujours la même sur le Df . . . ? Non effectivement ! f ' (x) sera forcément fonction de x !
Regarde le graphe complet de la courbe et tu observes que la tangente longeant Cf à sa pente qui varie partout, parfois > 0 et parfois < 0 ...
De plus, une pente de - 2 signifie que si tu te déplaces de 1 sur la droite alors au bout du 1 tu te déplaces de 2 vers le bas . . .

[Norma]

Bon j'ai déjà un problème sur la dérivée... Je cherche la dérivée de

Et je trouve

Et pour

Je trouve également f'(x)=-2

En fait,

Donc,


et [/quote]


Ok.. alors ce qui est "fou", c'est que dans le cours cette formule n'apparaît pas... en tout cas pas directement,

je n'ai que

En farfouillant et en trouvant un seul et unique exemple, je retrouve ta formule mais directement appliquée, pas sous la forme u-v...