Fonction/dérivées/équations polynomiales

[laetidom]

Comment je peux rajouter un tableau à mon poste pour te montrer ce que j'ai fais?

J'utilise l'hébergeur d'images ImagiLIVE, je copie l'adresse qu'il me créé, je viens dans le post, j'ouvre Img, je colle l'adresse, j'envoie le post

[Norma]

je ne sais pas si on voit bien. Le première ligne correspond à la version "simple" que j'ai sur l'étude des signes dans le cours, et en dessous-ce que tu m'as donné, donc ça colle. Manque les limites oui (je vais essayer)

[laetidom]

Ca a l'air de coller !

Les limites que tu as déjà calculées et la valeur de y en x=0

Une fois le tableau de variations complet, ça nous permet de dessiner l'allure de la courbe à main levée en quelques secondes, but : avec un schéma synoptique, en un clin d'œil pouvoir observer le comportement de la fonction sur le Df.

[Norma]

J'suis un peu(beaucoup) brouillon dans mon brouillon, désolée.

[laetidom]

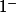
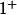
On avait pas calculé une limite en +/- égale à 1 ?, il me semble . . .et si tu calcules bien, confirmée sur le graphe, en elle est de (la courbe se rapproche par dessous) et en elle est de (la courbe se rapproche par dessus)

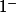
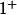
en et en la limite est de

[Norma]

Je l'ai mal disposé dans le tableau?

[laetidom]

Je l'ai mal disposé dans le tableau?

Oui, regarder le graphe te permet aussi de contrôler.

[Norma]

ok je vois, mais ducoup je ne sais pas ce que je dois mettre à la place de tes points d'interrogations à gauche et à droite des traits verticaux indiquant 1 comme valeur interdite.

[laetidom]

ok je vois, mais ducoup je ne sais pas ce que je dois mettre à la place de tes points d'interrogations à gauche et à droite des traits verticaux indiquant 1 comme valeur interdite.

à gauche et à droite la courbe vient de

[Norma]

Alors c'est ce que je me suis dis mais.. je vais passer pour une neuneu, on est d'accord que l'infini est une borne "indéterminée", là-haut ta courbe elle doit bien redescendre à partir d'un point... oui l'infini... enfin pour moi c'est pas logique, si la borne est infini.. ben la courbe ne revient pas, puisqu'elle continue de monter????!!! J'suis con ouuu??

Et je fais comment pour représenter ça graphiquement? Ca ne sera jamais précis ? Même si l'idée est de pouvoir juste avoir un rapide état des lieux, je dois bien me baser sur des valeurs, pour toute valeur x, y = ?? Combien de valeur triviale de x je prends à ce moment là ?

[laetidom]

Alors c'est ce que je me suis dis mais.. je vais passer pour une neuneu, on est d'accord que l'infini est une borne "indéterminée", là-haut ta courbe elle doit bien redescendre à partir d'un point... oui l'infini... enfin pour moi c'est pas logique, si la borne est infini.. ben la courbe ne revient pas, puisqu'elle continue de monter????!!! J'suis con ouuu??

Le cheminement de la courbe vient de -inf, chemine, se rapproche de x=1 jusqu'à +inf sans jamais atteindre x=1,
puis elle vient de +inf très proche de x=1 et s'en éloigne au fur et à mesure pour venir se rapprocher sans l'atteindre y=1

Et je fais comment pour représenter ça graphiquement? Ca ne sera jamais précis ? Même si l'idée est de pouvoir juste avoir un rapide état des lieux, je dois bien me baser sur des valeurs, pour toute valeur x, y = ?? Combien de valeur triviale de x je prends à ce moment là ?

1/0 interdit
1/0.000000000001 existe et tend
1/-0.000000000001 existe et tend

c'est le chapitre des limites

la pointe du crayon posée au bord de x=1 (interdit) et tu descends tout en s'éloignant de cette asymptote . . .

[Norma]

ok, je vois mieux. Autres questions: si les deux limites calculer pour et valent 1, l'asymptote est donc horizontale en y=1 c'est bien ça ? Pourquoi plus tôt on parlait alors d'asymptote verticale?

Pour T2 j'en suis revenue à ton graphique: j'ai donc mal réduis mon calcul ? Il faut laisser sur 27 ? De plus pour tracer les tangente je me sers du tableau de valeurs c'est bien ça ?

[laetidom]

ok, je vois mieux. Autres questions: si les deux limites calculer pour l'asymptote est donc horizontale en y=1, juste ? Oui !

Pour T2 j'en suis revenue à ton graphique: j'ai donc mal réduis mon calcul ? Il faut laisser sur 27 ? Et oui !, tu as simplifier par 27 d'un côté de l'équation mais de l'autre ? De plus pour tracer les tangente je me sers du tableau de valeurs c'est bien ça ? Si tu veux, c'est le plus simple à expliquer : 2 points suffisent.

[Norma]

Ok, bon, je crois que je tiens le bon bout, mais pfffff je vais mettre tout ça au propre!

Merci 1000 fois

[laetidom]

Ok, bon, je crois que je tiens le bon bout, mais pfffff je vais mettre tout ça au propre!

Merci 1000 fois

Nous " compatissons " (sourire) mais c'est la seule méthode pour que ça rentre ! Bon courage !
Si tu as besoin de précisions, n'hésites pas demain ou les jours qui suivent ! . . .
Bonne soirée !

[Norma]

Merci! Je vais éviter de te solliciter tous les jours... tu as aussi une vie ^^

[laetidom]

Merci! Je vais éviter de te solliciter tous les jours... tu as aussi une vie ^^

C'est gentil !, Si ce n'est pas moi ça sera un(e) autre collègue, mais comme on est là par passion . . .