Fonction cosinus et sa réciproque
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Lorisfaragou » 01 Oct 2021, 16:55
par Lorisfaragou » 01 Oct 2021, 16:55
Bonjour à tous, j'aimerai avoir de l'aide sur un exercice de trigo svp !
voici l'énoncé:
Écrire x=arcsin(sin(−12.8)) sous la forme x=a+bπ avec a et b des nombres rationnels.
Je ne sais pas comment répondre à cette question sans l'aide de ma calculatrice..

merci d'avance pour l'aide
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Oct 2021, 17:43
par GaBuZoMeu » 01 Oct 2021, 17:43
Bonjour,
Revenir à la définition de l'arcsinus :
 \Leftrightarrow -\pi/2\leq x\leq \pi/2 \text{ et } \sin(x) = y)
.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 01 Oct 2021, 19:02
par tournesol » 01 Oct 2021, 19:02
La fonction sinus est bijective de [-pi/2;pi/2] sur [-1;1]
Arcsin est sa fonction réciproque ,donc pour tout x dans [-pi/2;pi/2] , arcsin(sin(x))=x
Il te suffit donc de calculer la mesure principale de -12,8 radians qui elle est dans ]-pi/2;pi/2]
Tu calcules la mesure principale en tours : elle doit être dans ]-1/2;1/2]
1 tour , c'est 2pi radians donc -12,8 radians=-12,8/2pi tours= -2,035... tours
Tu dois donc ajouter 2 tours pour être dans ]-1/2;1/2] , donc 4pi radians à ton angle .
 par Lorisfaragou » 02 Oct 2021, 08:24
par Lorisfaragou » 02 Oct 2021, 08:24
Mais lorsque j’ai x=arccos(cos(-4.9)) a mettre sous la meme forme, comment puis-je faire ça de tete ?
Merci d’avance
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 02 Oct 2021, 08:58
par tournesol » 02 Oct 2021, 08:58
Détermine sur quel intervalle on a arccos(cos(x))=x , puis même méthode .
 par Lorisfaragou » 02 Oct 2021, 09:04
par Lorisfaragou » 02 Oct 2021, 09:04
tournesol a écrit:Détermine sur quel intervalle on a arccos(cos(x))=x , puis même méthode .
Et pareil si l’on a x=arccos(sin(-5,4)) ?
Car là je ne sais pas comment trouver son domaine de définition
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 02 Oct 2021, 09:30
par tournesol » 02 Oct 2021, 09:30
cos(pi/2-x)=sin(x) pour tout x
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 02 Oct 2021, 10:42
par GaBuZoMeu » 02 Oct 2021, 10:42
Bonjour,
Revenir à la définition de l'arccosinus :
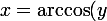 \Leftrightarrow 0\leq x\leq \pi \text{ et } \cos(x) = y)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités