Fonction continue sur un intervalle de R
40 messages
- Page 2 sur 2 - 1, 2
Re: fonction continue sur un intervalle de R
Euhh j'en sais rien mais ça me parait faux comme propriétés. Ca peut-être une union d'intervalle aussi non ?
Re: fonction continue sur un intervalle de R
Salut
Tu est vraiment sûr que, par exemple l'image réciproque de l'intervalle [4,9] par la fonction (continue) x->x^2 est un intervalle ? (voire l'image réciproque de l'intervalle [1,2] par la fonction cosinus...)
Heuuuuuu...aviateur a écrit:Il m'avait semblé que "l'image réciproque d'un intervalle par une fonction continue est un intervalle " était un résultat de base concernant les fonctions continues.
Tu est vraiment sûr que, par exemple l'image réciproque de l'intervalle [4,9] par la fonction (continue) x->x^2 est un intervalle ? (voire l'image réciproque de l'intervalle [1,2] par la fonction cosinus...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: fonction continue sur un intervalle de R
En effet, après bon peut etre qu'il voulait dire qu'on peut se restreindre de tel façon à ce que ce soit un intervalle ...mais c'est le but de ce post.
Soit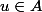 .
.
Je considère deux ensembles : = \{ l=|u-g| ; g<u \ et\ g \in B\}) et
et =\{ l'=|u-g| ; g>u \ et\ g \in B \})
Au moins l'un de ces deux ensembles est non vide, et admet donc une borne inférieur.
On appelle un tel ensemble pour pas alourdir les notations. On note
un tel ensemble pour pas alourdir les notations. On note  sa borne inférieur. On suppose qu'il n'admet pas de minimum.
sa borne inférieur. On suppose qu'il n'admet pas de minimum.
On pose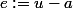 (ou
(ou 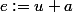 ). On a clairement
). On a clairement 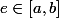
Par propriété de la borne inférieur et continuité (bon là je sais pas comment justifier ça), on a alors=c) .
.
Impossible par continuité. Donc admet un minimum.
admet un minimum.
On se ramène alors à ma preuve précédente.
Soit
Je considère deux ensembles :
Au moins l'un de ces deux ensembles est non vide, et admet donc une borne inférieur.
On appelle
On pose
Par propriété de la borne inférieur et continuité (bon là je sais pas comment justifier ça), on a alors
Impossible par continuité. Donc
On se ramène alors à ma preuve précédente.
Re: fonction continue sur un intervalle de R
Finalement pour justifier l'incompatibilité avec la continuité , on combine la caractérisation séquentiel des limites et les propriétés de la borne inférieur. Et ça marche plutôt bien
Re: fonction continue sur un intervalle de R
Bonjour
@ben 314. Tu as tout à fait raison. Heureusement que tu est là pour corriger des erreurs aussi affreuses.
J'essaie de guider Arist pas à pas, sans forcément avoir fait l'exercice, un peu en direct. C'est un peu une source d'erreurs. Néanmoins c'est impardonnable.
Donc milles excuses pour cette faute grossière.
Ceci étant dit, pour ton deuxième exemple, il me semble que l'ensemble vide est considéré comme un intervalle.?
@ben 314. Tu as tout à fait raison. Heureusement que tu est là pour corriger des erreurs aussi affreuses.
J'essaie de guider Arist pas à pas, sans forcément avoir fait l'exercice, un peu en direct. C'est un peu une source d'erreurs. Néanmoins c'est impardonnable.
Donc milles excuses pour cette faute grossière.
Ceci étant dit, pour ton deuxième exemple, il me semble que l'ensemble vide est considéré comme un intervalle.?
Re: fonction continue sur un intervalle de R
@arist a dit :
Ravis de voir que tout le monde s'en fout joyeusement
Non je ne crois pas que tout le monde s'en fout. Je ne pense pas que c'est la mentalité du forum.
Au contraire.
Il y a plusieurs explications n'oublie que l'on travaille encore et (où) que l'on a d'autres activités aussi.
Personnellement j'ai commencé à t'aider et je pense revenir sur cet exercice après midi dès que j'aurai un peu de temps. Un peu de patience donc.
Re: fonction continue sur un intervalle de R
Rebonjour
Je fais la synthèse:
Ta démonstration pose problème car par définition de tes ensembles A et B, tu sous-entends que les intervalles J et L sont bornés ce qui ne fait pas parties des hypothèses. Donc je ne relie pas ton post d'hier de 16h 03, car, même si je pense que l'idée est bonne, la démonstration sera restrictive.
Je propose donc ceci et à vérifier. Soit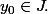
Comme) , il existe
, il existe 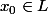 tel que
tel que =y_0)
On considère maintenant l'ensemble des couples
des couples
\in (R_+)^2) tels que
tels que

\subset J)
Il reste à voir les points suivants:
1. est non vide.
est non vide.
2. Si\in \Omega) tout couple
tout couple ) tel que
tel que
 est dans \Omega
est dans \Omega
3. La fermeture de est de la forme
est de la forme 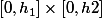
( avec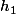 ou
ou 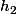 éventuellement égaux à
éventuellement égaux à 
4. L'intervalle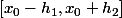 répond à la question.
répond à la question.
(si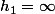 alors comprendre
alors comprendre 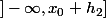 )
)
Je fais la synthèse:
Ta démonstration pose problème car par définition de tes ensembles A et B, tu sous-entends que les intervalles J et L sont bornés ce qui ne fait pas parties des hypothèses. Donc je ne relie pas ton post d'hier de 16h 03, car, même si je pense que l'idée est bonne, la démonstration sera restrictive.
Je propose donc ceci et à vérifier. Soit
Comme
On considère maintenant l'ensemble
Il reste à voir les points suivants:
1.
2. Si
3. La fermeture de
( avec
4. L'intervalle
(si
Modifié en dernier par aviateur le 17 Nov 2017, 11:12, modifié 1 fois.
Re: fonction continue sur un intervalle de R
Salut, Qu'est-ce que tu appelles fermeture de  ? Par contre ta propositions me semble quand même fausse. On peut très bien avoir pris un
? Par contre ta propositions me semble quand même fausse. On peut très bien avoir pris un  tel que pour n'importe quel intervalle
tel que pour n'importe quel intervalle 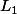 contenant
contenant  , on ne vérifie pas
, on ne vérifie pas =J)
De ce que j'ai vu en cours (niveau L1), un intervalle réel fermé est un segment. Bon sinon j'ai réussis ma preuve en restant sur mon idée de départ (et en considérant en effet que mes ensembles sont bornés).
Sans la détailler :
On prend tel que
tel que=d) (on a
(on a 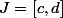 )
)
Je considère ces deux ensembles=c \ et \ g<u\}) et
et =c \ et \ g>u\}) . Il y en a forcément un non vide, que l'on note
. Il y en a forcément un non vide, que l'on note  . On considère
. On considère 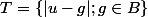 . On note
. On note  sa borne inférieur. On montre que
sa borne inférieur. On montre que  admet un minimum : pour ce faire on suppose qu'il n'en admet pas, puis on construit par propriété de la borne inférieur une suite
admet un minimum : pour ce faire on suppose qu'il n'en admet pas, puis on construit par propriété de la borne inférieur une suite  qui tend vers
qui tend vers ( ou
( ou 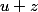 ) si on raisonne sur
) si on raisonne sur 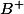 ( ou sur
( ou sur 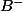 ). Et on montre alors qu'on a des problèmes de continuité de
). Et on montre alors qu'on a des problèmes de continuité de  en
en  (ou en
(ou en 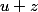 ) , par caractérisation séquentielle de la limite, car on aurait alors
) , par caractérisation séquentielle de la limite, car on aurait alors =c) (ou
(ou =c) )Or comme la fonction est continue, par l'absurde on a que
)Or comme la fonction est continue, par l'absurde on a que  admet bien un minimum. Et on se ramène a ma première preuve qui se base sur l'existence de ce minimum.
admet bien un minimum. Et on se ramène a ma première preuve qui se base sur l'existence de ce minimum.
De ce que j'ai vu en cours (niveau L1), un intervalle réel fermé est un segment. Bon sinon j'ai réussis ma preuve en restant sur mon idée de départ (et en considérant en effet que mes ensembles sont bornés).
Sans la détailler :
On prend
Je considère ces deux ensembles
Re: fonction continue sur un intervalle de R
Bonjour @Arist
1. tu as dit que ma proposition est fausse car "On peut très bien avoir pris un tel x_0......." mais cela ne veut rien dire. Donc tu peux démonter ma suggestion (est non "proposition" au sens mathématiques du terme) mais en disant des choses qui ont un sens s'il te plait.
2. Ma "proposition" n'est pas une proposition, c'est à dire que je suggère une démonstration en indiquant les étapes mais chaque étape est encore à vérifier (i.e à justifier).
3. Tu as dit
De ce que j'ai vu en cours (niveau L1), un intervalle réel fermé est un segment.
Pour moi c'est faux ou tout au moins il y a ambiguité sur le vocabulaire.
En effet si a et b sont des réels on dit que [a,b[ est fermé à droite et ouvert à gauche, mais ce n'est un intervalle fermé.
Un intervalle tel que
En conclusion: Je reste d'accord que ton idée de départ était bonne mais il y avait des choses à justifier, comme l'existence de m.
Ensuite tu as supposé que les intervalles fermés étaient des intervalles fermés bornés.
Mais ce n'est pas comme cela que j'ai vu l'énoncé. Pour moi, les intervalles était des fermés donc pas forcément bornés.
Il faut au moins être d'accord sur l'énoncé, d'autant plus que je ne vois pas pour l'instant la raison de se restreindre aux intervalles fermés bornés.
Re: fonction continue sur un intervalle de R
J'ai justifié l'existence de  dans mon précédent message. S'il y a un point qui te semble peu clair, je peux tenter de le justifier.
dans mon précédent message. S'il y a un point qui te semble peu clair, je peux tenter de le justifier.
-Ce petit résultat d'un lème dont la démo est "laissé au lecteur" vient d'un poly dont le but est de démontrer le Théorème de Charkovskii, plus connu sous le nom de son corollaire "période 3 implique chaos", et de ce que j'ai compris, on travail avec des intervalles bornés de R.
-Pour moi "fermé"="segment". Mais je me suis manifestement trompé. Cela dit, il me semble que ce que j'ai fais marche quasiment de la même façon quand on travail juste sur des intervalles bornés qui ne sont pas forcément des segments.
-Je vais avoir du mal à bien te justifier pourquoi j'ai dit que c'est faux, car je ne sais pas ce que veux dire "fermeture de " ? Par contre, de ce que j'ai compris (manifestement mal), tu considères
" ? Par contre, de ce que j'ai compris (manifestement mal), tu considères 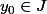 . On a bien l'existence de
. On a bien l'existence de 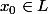 tel que
tel que =y_{0}) . Et ensuite tu montre alors qu'il existe un intervalle
. Et ensuite tu montre alors qu'il existe un intervalle 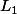 de
de  avec
avec 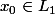 , tel que
, tel que =J) . Si c'est le cas, on peut voir en faisant un dessin, que dans beaucoup de cas, il n'existe pas un tel intervalle pour un
. Si c'est le cas, on peut voir en faisant un dessin, que dans beaucoup de cas, il n'existe pas un tel intervalle pour un 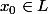 quelconque , sans condition supplémentaire que l'existence de
quelconque , sans condition supplémentaire que l'existence de 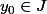 tel que
tel que =y_{0}) (c'est la seul condition que tu imposes sur
(c'est la seul condition que tu imposes sur  ).
).
-Ce petit résultat d'un lème dont la démo est "laissé au lecteur" vient d'un poly dont le but est de démontrer le Théorème de Charkovskii, plus connu sous le nom de son corollaire "période 3 implique chaos", et de ce que j'ai compris, on travail avec des intervalles bornés de R.
-Pour moi "fermé"="segment". Mais je me suis manifestement trompé. Cela dit, il me semble que ce que j'ai fais marche quasiment de la même façon quand on travail juste sur des intervalles bornés qui ne sont pas forcément des segments.
-Je vais avoir du mal à bien te justifier pourquoi j'ai dit que c'est faux, car je ne sais pas ce que veux dire "fermeture de
Re: fonction continue sur un intervalle de R
Bonjour
Que l'on se comprenne bien, l'idée de proposer une démonstration différente de la tienne est de considérer aussi les intervalles qui sont des fermés non bornés.
D'autre part je n'ai pas été jusqu'au bout de la démonstration mais j'ai proposé les différentes étapes qui doivent être justifiées correctement. Ce que je n'ai pas encore fait. Mais je pense que l'idée est correcte.
Au passage je me demande s'il n'y a pas une démonstration plus simple.
Maintenant concernant je ne comprends pas ton argument où encore il faudrait un exemple précis.
je ne comprends pas ton argument où encore il faudrait un exemple précis.
 ce n'est pas n'importe quoi. En effet
ce n'est pas n'importe quoi. En effet ) est dans J. Ensuite je considère tous les intervalles de la forme
est dans J. Ensuite je considère tous les intervalles de la forme 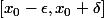 qui sont dans L et dont l'image par
qui sont dans L et dont l'image par
f est incluse dans J.
L'idée de la démonstration est de prendre "le plus grand de ces intervalles" qui est donné par la fermeture de
 (par définition la fermeture de
(par définition la fermeture de  est le plus petit fermé qui contient
est le plus petit fermé qui contient  ).
).
Que l'on se comprenne bien, l'idée de proposer une démonstration différente de la tienne est de considérer aussi les intervalles qui sont des fermés non bornés.
D'autre part je n'ai pas été jusqu'au bout de la démonstration mais j'ai proposé les différentes étapes qui doivent être justifiées correctement. Ce que je n'ai pas encore fait. Mais je pense que l'idée est correcte.
Au passage je me demande s'il n'y a pas une démonstration plus simple.
Maintenant concernant
f est incluse dans J.
L'idée de la démonstration est de prendre "le plus grand de ces intervalles" qui est donné par la fermeture de
Re: fonction continue sur un intervalle de R
Du coup qu'est ce qu'un fermé ?
Le truc c'est que le que tu utilise dans ta démo est fixé dès le départ.
que tu utilise dans ta démo est fixé dès le départ.
A partir de là, la démonstration qui a pour but de construire (ou de montrer l'existence) d'un ensemble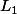 contenant
contenant  et qui vérifie
et qui vérifie =J) , doit marcher pour n'importe quel
, doit marcher pour n'importe quel  qui vérifie les conditions que tu as imposé au départ pour le "choix" de cet
qui vérifie les conditions que tu as imposé au départ pour le "choix" de cet  . Or on voit bien sur un dessin qu'il faut plus de conditions sur
. Or on voit bien sur un dessin qu'il faut plus de conditions sur  . Je joins une capture d'écran pour illustrer ce que je veux dire. Ce sera plus parlant.
. Je joins une capture d'écran pour illustrer ce que je veux dire. Ce sera plus parlant.
On a ici le graphe d'une application continu de
continu de 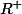 dans
dans  . dans On pose
. dans On pose 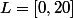 .On a
.On a ) est un intervalle (borné qui plus est). On pose
est un intervalle (borné qui plus est). On pose 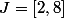 . On a
. On a ) .
.
Soit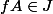 .Il existe
.Il existe 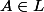 tel que
tel que =fA) . On s’aperçoit qu'il n'existe pas d'intervalle
. On s’aperçoit qu'il n'existe pas d'intervalle 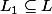 tel que
tel que 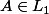 et
et =J) . Pourtant j'ai bien respecté toute les conditions que ta démo imposait sur
. Pourtant j'ai bien respecté toute les conditions que ta démo imposait sur  .
.
Le truc c'est que le
A partir de là, la démonstration qui a pour but de construire (ou de montrer l'existence) d'un ensemble
On a ici le graphe d'une application
Soit
Re: fonction continue sur un intervalle de R
D'accord c'est clair.
Donc je pense qu'il faut revenir à ta démonstration et voir si on peut l'adapter au cas général des intervalles qui sont des fermé et non bornés.
Donc je pense qu'il faut revenir à ta démonstration et voir si on peut l'adapter au cas général des intervalles qui sont des fermé et non bornés.
Re: fonction continue sur un intervalle de R
aviateur a écrit:Il m'avait semblé que "l'image réciproque d'un intervalle par une fonction continue est un intervalle " était un résultat de base concernant les fonctions continues.
voici un contre exemple
par contre l'image réciproque d'un ouvert est un ouvert.
l'image directe d'un intervalle (resp. d'un compact) est un intervalle (resp. un compact)
Re: fonction continue sur un intervalle de R
@Mathelot là le problème est réglé. Merci de ne plus me rappeler cette erreur!!!
On cherche maintenant à voir si le résultat est encore vrai pour des intervalles J de la forme
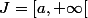
On cherche maintenant à voir si le résultat est encore vrai pour des intervalles J de la forme
Re: fonction continue sur un intervalle de R
Non, pour des intervalles non bornés, c'est clairement faux :
Si on prend f:R->R;x->x.sin(x) (qui est non seulement continue, mais même C^infini sur R) et J=L=[0,+oo[ alors f(L)=]-oo,+oo[ donc on a bien J contenu dans f(L) et il est bien clair qu'il n'existe aucun intervalle L1 tel que f(L1)=J=[0,+oo[.
Bref, je sais pas où Arist a récupéré son truc sur le théorème de Charkovskii, mais, clairement dans tout le texte, il faut prendre l'expression "intervalle fermé" dans le sens "Lycée" du terme, c'est à dire "intervalle fermé borné" et pas dans le sens topologique de l'expression "fermé".
De toute façon, le résultat en question, c'est juste un petit lemme préliminaire du théorème et lorsqu'on l'applique dans le théorème de Charkovskii, c'est bien avec des intervalles fermés bornés.
Si on prend f:R->R;x->x.sin(x) (qui est non seulement continue, mais même C^infini sur R) et J=L=[0,+oo[ alors f(L)=]-oo,+oo[ donc on a bien J contenu dans f(L) et il est bien clair qu'il n'existe aucun intervalle L1 tel que f(L1)=J=[0,+oo[.
Bref, je sais pas où Arist a récupéré son truc sur le théorème de Charkovskii, mais, clairement dans tout le texte, il faut prendre l'expression "intervalle fermé" dans le sens "Lycée" du terme, c'est à dire "intervalle fermé borné" et pas dans le sens topologique de l'expression "fermé".
De toute façon, le résultat en question, c'est juste un petit lemme préliminaire du théorème et lorsqu'on l'applique dans le théorème de Charkovskii, c'est bien avec des intervalles fermés bornés.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: fonction continue sur un intervalle de R
Bon bah il me semble que le sujet est presque clos du coup. Le seul truc que je ne sais pas encore faire rigoureusement pour finaliser ce que j'ai fais, c'est si on a un un ensemble admettant une borne inférieur et n'admettant pas de minimum : comment construire une suite convergente vers cette borne inférieur ? Je vois bien que c'est possible puisqu'on pourra prendre des éléments de l'ensemble aussi proche qu'on veut de la borne inférieur, mais je sais pas trop le formaliser.
Re: fonction continue sur un intervalle de R
A mon avis, ça provient du fait que tu as uniquement une idée "intuitive" de ce qu'est la borne inférieure (ce qui est déjà très bien...).
Si tu prend une définition "bien propre" de ce qu'est une borne inférieure, quel qu'elle soit (la définition), ça doit "couler de source" comme résultat.
Bref, pour toi, c'est quoi la définition "propre" d'une borne inférieure ?
Si tu prend une définition "bien propre" de ce qu'est une borne inférieure, quel qu'elle soit (la définition), ça doit "couler de source" comme résultat.
Bref, pour toi, c'est quoi la définition "propre" d'une borne inférieure ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: fonction continue sur un intervalle de R
Non t'inquiète, je connais la définition propre de la borne inférieur (enfin j’espère) ainsi que ses propriétés. C'est le plus petit des minorants il me semble. Je connais aussi bien la propriété avec les epsilon tout ça tout ça ...mais ....
Bon bah finalement ouais ça va je sais faire. Je viens de m'apercevoir que c'était trivial en écrivant. Merci bien
Problème réglé
Bon bah finalement ouais ça va je sais faire. Je viens de m'apercevoir que c'était trivial en écrivant. Merci bien
Problème réglé
40 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
