Fonction continue+injective=>ouverte

[ffpower]

Voila un résultat qui m a toujours étonné:une fonction continue,injective de R^n dans R^n est forcément ouverte.J ai éssayé par tous les moyens de le démontrer sans succes,j ai cherché des références mais la seule que j ai trouvé ct au 20eme chapitre d un livre de topo algébrique,donc bof..J aimerai donc savoir si qqun ici connait une demo a peu pres abordable de ce résultat(ou un lien vers une demo abordable)

[regis183]

bonjours, pourrais tu préciser la définition exacte d'une "fonction ouverte" stp?

[busard_des_roseaux]

bjr,

une application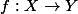 est ouverte si l'image directe d'un ouvert est un ouvert. Si f est continue et injective, ceçi assure que l'application réciproque , est continue pour la topologie induite sur f(X).

voiçi quelques indications pour la démo dans le cas de dans :

Si O est un ouvert de (ensemble de départ)
O est la réunion d'intervalles ouverts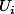

On a l'égalité ensembliste:


Il suffit donc de montrer que l'image d'un intervalle ouvert est un intervalle
ouvert.

L'image d'un intervalle est un intervalle, ceçi résulte du TVI.

Si f est injective,f est un morphisme d'ordre, ie, elle est nécéssairement
croissante ou décroissante. Supposons la croissante:
Comme elle conserve l'ordre et est continue, on a:



C'est donc une application ouverte. Il doit y avoir une démonstration
dans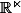 pour les applications différentiables
à différentielle injective, donc bijective à cause des dimensions.

les étapes sont:
- différentielle injective donc bijective
- différentielle bijective donc f est localement bijective d'inverse
le thm des fonctions implicites donne la continuité de .
f est localement ouverte donc ouverte, puisque c'est une propriété locale comme la continuité ou la différentiabilité.

[ffpower]

dsl mais la premiere étape est fausse(ya qu a prendre x->x^3,la differentielle en 0 n est pas bij puisque nulle)

EDIT:et au fait normalement,la différentiabilité n est supposée^^

[busard_des_roseaux]

dsl mais la premiere étape est fausse(ya qu a prendre x->x^3,la differentielle en 0 n est pas bij puisque nulle)

EDIT:et au fait normalement,la différentiabilité n est supposée^^

la différentielle de n'est pas injective en tout point. C'est un exemple intéressant mais qui ne fait pas partie de mon propos.

[busard_des_roseaux]

Je traitais uniquement le cas particulier : df(x) injective en tout point. Ce n'était pas une conséquence des hypothèses mais une hypothèse supplémentaire.

[ffpower]

ok j avais mal lu..a vrai dire j ai d ailleurs essayer d adapter la preuve de l inversion locale,genre en remplacant le theoreme de point fixe des applications contractantes par brouwer,mais c est difficile de trouver des compacts stables..