Fonction beta d'Euler

[CC_]

Bonjour,

J'ai besoin de vos lumières à propos de la fonction beta d'Euler.
On la définit par .

Pourriez-vous m'aider à établir que B(x+1,y) = x/x+y B(x,y) ? J'ai essayé par IPP mais ça n'aboutit pas... Y a-t-il un changement de varaibles à faire, ou autre chose ?..

De plus, comment calcule-t-on B(1/2,1/2) ?

Merci !

[Sa Majesté]

Bonjour,

J'ai besoin de vos lumières à propos de la fonction beta d'Euler.
On la définit par .

Pourriez-vous m'aider à établir que B(x+1,y) = x/x+y B(x,y) ? J'ai essayé par IPP mais ça n'aboutit pas...

J'ai abouti en 2 étapes :
1) IPP => 1ère relation
2) Faire intervenir artificiellement un dans l'intégrale puis Re-IPP => 2ème relation
1ère + 2ème relations => le résultat à démontrer

[nuage]

Salut,
avec de vieux souvenirs :
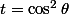
Tu peux essayer de poser avec .
Pour calculer B(1/2;1/2)ça marche, pour le reste aussi, je crois, mais je n'ai pas vérifié.

[Sa Majesté]

De plus, comment calcule-t-on B(1/2,1/2) ?

Pense à un changement de variables de type trigo ...
EDIT Grillé par nuage ... mais je n'ai pas donné le changement de variables !! :zen:

[CC_]

Bonjour tous les deux,

Salut,
avec de vieux souvenirs :
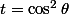
Tu peux essayer de poser avec .
Pour calculer B(1/2;1/2)ça marche, pour le reste aussi, je crois, mais je n'ai pas vérifié.

J'ai trouvé grâce à cette méthode, merci !
Je vais essayer de suivre vos conseils pour la relation entre B(x+1,y) et B(x,y).

A bientôt !

[Sa Majesté]

J'ai trouvé grâce à cette méthode, merci !

Ah bon ? Pas moi !!

[nuage]

Salut,
il me semble que
Et ce ce que semble montrer la méthode que j'ai donnée :

Sauf erreur de ma part.

[Sa Majesté]

Déolé je me suis lamentablement vautré ...
J'ai fait
C'est ballot ... :marteau: