La fonction Béta d' Euler

[lieutenant R]

Bonjours à tous j ai un p'tit problème sur la fonction Béta d' Euler

Soit B(x,y) = intégrale(0 à 1) (U^(x-1))*(1-U)^(y-1)du Avec (x,y) réels



1°) La première question concerne le domaine de définition de B à priori je dirai que c est R ...



2°) Sachant que G(x) = intégrale (o à l'infini)exp(-t)*t^(x-1)dt il faut montrer que
B(x,y) = ( G(x) * G(y) ) / ( G(x+y) ) visiblement il faut faire un changement de variable mais je vois pas lequel... :stupid_in



3°) La dernière question consiste à Calculer
l' intégrale( 0 à 1 )(t^n)*((1-t)^n)dt
je pense qu' en trouvant la résolution de la question 2°) on y répond sans problème ....



Merci de vos lumières Raph :++:

[lieutenant R]

alala cette fonction Béta ... personne peut nous aider ??? :mur: :mur: :we:

[alavacommejetepousse]

bonjour

a priori je dirais qu 'une fonction de 2 variables réelles est nécessairement définie sur une partie de R^2

[ThSQ]

1°) La première question concerne le domaine de définition de B à priori je dirai que c est R ...

Déjà, comme dit, c'est une partie de R² et comment tu calcules B(-1,-1) par exemple ?

[cadi]

Bonjours à tous j ai un p'tit problème sur la fonction Béta d' Euler

Soit B(x,y) = intégrale(0 à 1) (U^(x-1))*(1-U)^(y-1)du Avec (x,y) réels



1°) La première question concerne le domaine de définition de B à priori je dirai que c est R ...



2°) Sachant que G(x) = intégrale (o à l'infini)exp(-t)*t^(x-1)dt il faut montrer que
B(x,y) = ( G(x) * G(y) ) / ( G(x+y) ) visiblement il faut faire un changement de variable mais je vois pas lequel... :stupid_in



3°) La dernière question consiste à Calculer
l' intégrale( 0 à 1 )(t^n)*((1-t)^n)dt
je pense qu' en trouvant la résolution de la question 2°) on y répond sans problème ....



Merci de vos lumières Raph :++:

non le domaine de definition de B est pour tout x,y> 0 mais pour l'autre question je suis bloquer comme toi

[ThSQ]

B(x,y) = ( G(x) * G(y) ) / ( G(x+y) )

Fubini + x+y=u, x/y=v

[lieutenant R]

c est a dire fubini ? c est un changement de variable dont tu parles ????


MERCI encore raf

[Pythales]

Essaye de calculer de 2 façons différentes l'intégrale :

[lieutenant R]

bha visiblement cela ne me donne rien de bien convainquant .... désolé pour le retard ! Quelqu' un aurai-t-il une autre suggestion ??


Merce à vous !

[Pythales]

Allez, un petit coup de pouce.
1ère façon de calculer :
Dans l'intégrale du message 8, pose et
Que devient l'intégrale ?
2ème façon de calculer :
Passe en polaires, sachant que dans l'expression de on peut poser

[jver]

bonjour

a priori je dirais qu 'une fonction de 2 variables réelles est nécessairement définie sur une partie de R^2

En l'occurrence, beta est défini, tout x,y de C, si je ne m'abuse. Mais, je ne me rappelle plus, si c'est par prolongement analytique

[jver]

En l'occurrence, beta est défini, tout x,y de C, si je ne m'abuse. Mais, je ne me rappelle plus, si c'est par prolongement analytique

Je dis des bêtises!. beta est défini pour x et y complexes, non pour tout x,y complexes!

[jver]

En fait, ce n'est pas si évident que cela, de montrer que . Classique, mais pas totalement évident, selon moi.
D'abord, tu peux montrer que . Pour cela, tu fais le changement s=pt dans la définition de
Si on pose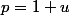 et 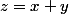, on obtient:


Ensuite, dans ta définition de beta, tu fais le changement de variables

On obtient ainsi:


Tu substitues et obtiens:


et on se rapproche de:


Maintenant, si quelqu'un a une méthode plus rapide, voire plus élégante, je suis preneur.

Maintenant, le comportement, pour x et y positifs, pas de problèmes (pour Re(x) et Re(y, ...). Sinon, pour x ou y négatifs est défini si x et y ne sont pas entiers négatifs et si x>0, non entier n'est pas défini, mais peut être défini par continuité comme étant égal à 0; pour n entier positif, je ne sais pas trop comment on fait (va falloir réfléchir), car il me semblait pouvoir montrer que est infini; ce n'est pas l'avis de mupad, qui me donne:



...

Déconne-je?

[jver]

Ce que je trouve mignon:

ce qui est facile, en passant à

[jver]

l'avis de mupad, qui me donne:



...

Désolé de m'auto-répondre, mais ...
Je reprends:


Mais pourquoi donc , dixit mupad ???

Si je prends, comme définition , cela ne m'avance guère !

Qui a une idée?

[jver]

Mais pourquoi donc , dixit mupad ???

Qui a une idée?

Je pose la question sur la liste de mupad. La réponse est clarissime:
" the reason is that
beta(x,1) = gamma(x)*gamma(1)/gamma(x+1) = 1/x
and thus beta(-1,1) = -1."

Mais je ne comprends toujours pas cette égalité :


Peut-être que la démonstration que j'ai indiquée de:
n'est-elle valable que pour x et y positifs, mais je ne vois pas très bien pourquoi.

Qui peut me donner un coup de main?

Merci d'avance.