Fonction affine et barycentre

[neuneu]

Bonjour je n'arrive pas à démontrer qu'une application est affine ssi elle conserve les barycentre.
Je ne vois pas du tout le lien et comment faire.
Quelqu'un pourrait-il m'aider s'il vous plaît?
Merci

[yos]

Affine pour toi c'est avec linéaire ?
En ce cas il suffit d'écrire les choses :

Supposons f affine et G barycentre de (A,a), (B,b)
et c'est fini.

Réciproque du même fût.

Bon il veut pas m'écrire le vecteur nul.

[fahr451]

Affine pour toi c'est avec linéaire ?

ah oui ça serait cool si la définition était: conserve le barycentre.
allez on prend celle là

[yos]

Ben non mais en prépa ils disent qu'une application affine c'est la composée d'une linéaire et d'une translation !!! Les bras m'en tombent à chaque fois.

[neuneu]

Merci yos j'ai compris le sens direct, mais pour la réciproque... je dis
Soit G barycentre de (A,a) et (B,b) donc aGA+bGB=0 tous des vecteurs
phi(aGA+bGB)=vect nul donc phi(aGA)=0 et phi(bGB)=0 ??
je ne comprends pas trop désolé

Comment fais tu pour écrire avec des vecteurs svp

[fahr451]

oui car l'accent est mis sur le linéaire

le géométrique étant marginal

garde tes bras , peuvent encore servir

[yos]

Comment fais tu pour écrire avec des vecteurs svp

Approche ton curseur de mes formules et tu verras ce que j'ai tapé.

La réciproque est un peu plus longue.
Essaie de lister dans l'ordre ce qu'on doit prouver.

[neuneu]

Désolé mais comme je le dis à chaque fois je ne peux pas être tout le temps connecté...mais merci !
merci yos j'ai vu pour les vecteurs ( j'ai mis au moins 20 minutes à écrire ce message !)
Soit G le barycentre de (A,a) et (B,b)
on a donc
mais est ce que je peux supposer que est linéaire? en fait dans la réciproque je ne sais pas de quoi j'ai le droit de partir
si oui je peux écrire:



cad ?

La condition de conservation du barycentre signifie que, si G est barycentre de (A,a) et (B,b),
alors f(G) est barycentre de (f(A),a) et (f(B),b). Nous avons donc :

donc
donc ???

merci d'avance

[yos]

Il faut que tu montres qu'il existe une application linéaire telle que .

1) Tu dois prouver que le vecteur ne dépend que du vecteur (et pas du couple (A,B)).

2) Ceci fait tu poses et tu montres que est linéaire.

Allons-y pour le premier point : on part de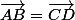 . Ca entraîne que [AD] et [BC] ont même milieu. Par conservation du barycentre, tu as [f(A)f(D)] et [f(B)f(C)] qui ont même milieu, donc . Et voilà!

Sauras-tu faire le second point?

[neuneu]

Salut yos, merci encore pour ton aide j'ai essayé de réfléchir à ce que tu m'a dit
pour le point 2)
on pose
on montre que est linéaire c'est à dire je dois montrer que

et


?

et
?

j'ai l'impression de ne rien démontrer, désolé!

[yos]

j'ai l'impression de ne rien démontrer, désolé!

Tu as le bon feeling, c'est déjà ça! :++:

Pour l'additivité, utilise le fait que tu as le choix du représentant (A,B) d'un vecteur. Donc au lieu de prendre (A,B) et (C,D), prends (A,B) et (B,C).

[neuneu]

je te remercie pour ton aide yos
je vais finir par abandonner je suis complètement larguée... j'arrive pas à voir ce que je peux écrire

est ce que je peux écrire
?

si oui après est ce que je peux dire:
?

et conclure par
?

est ce que au moins la démo pour est bonne? je n'ai pas trop d'espoir mais bon ..;

merci encore de prendre de ton temps pour m'expliquer

[yos]

[neuneu]

merci yos et désolé; j'espère ne pas trop t'avoir "énervé" à ne rien comprendre

[yos]

Ce n'est pas le fait que quelqu'un ne comprend pas qui peut m'énerver.
Par contre, l'absence de réponse aux réponses, les sujets mal posés, ... ça c'est autre chose. Au minimum ça me déçoit. Tu n'es pas dans ce cas.

Ici ton exo est pas méchant mais le plus dur est de voir ce qu'il faut prouver car c'est un peu abstrait.
Je ne sais pas comment vous voyez les barycentres mais on peut très bien écrire 5G=3A+2B pour exprimer que G est barycentre de (A,3),(B,2). Cela revient à fixer un point O puis à identifier un point M avec le vecteur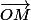 . C'est très pratique et cela montre bien que la conservation du barycentre 5f(G)=3f(A)+2f(B) équivaut à de la linéarité.

[neuneu]

re_salut, je comprends ce que tu me dis. Pour l'absence de réponses je comprends ce que tu dis. Je ne peux pas me connecter tout le temps à internet et donc je viens pas vague; mais j'essaye au maximum de remercier les gens qui prennent de leur temps pour me filer un petit coup de main.
Quand je le peux je vais dans "collège" ou "lycée" donner un petit coup de main à mon tour mais comme tu peux le constater par le nombre de messages écrit çà n'arrive pas très souvent.

Pour en revenir au barycentre, c'est comme tu l'as écrit que je l'ai vu; mais disons très honnêtement que je m'embrouille avec les applications affines et linéaires et c'est encore pire quand tu y rajoutes le barycentre. Quand je lis ce que tu me dis de faire je comprends mais je n'aurai certainement pas trouvé.

En tout cas merci encore pour ton aide
bonne soirée

[yos]

J'ai bien dit "tu n'es pas dans ce cas". Je parlais en général.
Bonne continuation.