Fermé
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 05 Avr 2008, 12:58
par fenecman » 05 Avr 2008, 12:58
Bonjour, voici ce qui me pose problème :
Soit
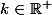
;
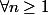
,
\in \mathbb{R^2} | (x-\frac{1}{n})^2 + (y-\frac{1}{n})^2 \le \frac{k^2}{n^2} \})
.
On me demande de trouver une CNS sur k pour que
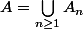
soit fermé.
J'ai essayé d'utiliser la propriété , A contient les limites de ses suites convergentes, mais sans succès :triste:.
Merci de votre aide.
 par alavacommejetepousse » 05 Avr 2008, 13:14
par alavacommejetepousse » 05 Avr 2008, 13:14
bonjour
je te conseille de dessiner concrètement les An et par exemple de voir une cs pour que l'union soit décroissante.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 13:39
par ThSQ » 05 Avr 2008, 13:39
Fais un dessin en séparant k > 1 et k < 1 :lol3:
 par alavacommejetepousse » 05 Avr 2008, 13:41
par alavacommejetepousse » 05 Avr 2008, 13:41
ThSQ a écrit:Fais un dessin en séparant k > 1 et k < 1 :lol3:
k = 1 n'est pas une valeur particulière
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Avr 2008, 13:48
par ThSQ » 05 Avr 2008, 13:48
alavacommejetepousse a écrit:k = 1 n'est pas une valeur particulière
Et après ? Ca permet de voir comment les A_n poussent.
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 05 Avr 2008, 13:54
par fenecman » 05 Avr 2008, 13:54
D'accord quand je fais un dessin je vois que pour k plus grand que racine de 2, l'union est decroissante. Mais pour montrer qu'elle est nécessaire, il va bien falloir que je prenne une suite convergente dans A et que je montre que sa limite est dans A ?
 par alavacommejetepousse » 05 Avr 2008, 13:56
par alavacommejetepousse » 05 Avr 2008, 13:56
ThSQ a écrit:Et après ? Ca permet de voir comment les A_n poussent.
il n 'y a pas lieu de regarder k = 1 les An ne poussent pas soit ils sont tous inclus dans A1 soit ils se décalent vers0 , 0 est alors ds l 'adhérence sans être ds l 'union
k = racine 2 est la valeur à regarder
 par alavacommejetepousse » 05 Avr 2008, 14:12
par alavacommejetepousse » 05 Avr 2008, 14:12
fenecman a écrit:D'accord quand je fais un dessin je vois que pour k plus grand que racine de 2, l'union est decroissante. Mais pour montrer qu'elle est nécessaire, il va bien falloir que je prenne une suite convergente dans A et que je montre que sa limite est dans A ?
si la condition n'est pas remplie regarde 0
0 est ds l 'adhérence et pas ds l'union donc l'union n est pas fermée
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 05 Avr 2008, 16:31
par fenecman » 05 Avr 2008, 16:31
Je comprends que si la condition n'est pas remplie alors 0 est dans l'adherence ,mais pas dans l'union ; Enfin je le vois sur la figure... Mais j'arrive pas à le montrer formellement.
De même , pour le fait que si k^2 > 2 alors l'union des A_n vaut A1, j'arrive pas à montrer formellement que les A_n sont décroissants...
C'est d'ailleurs assez désagréable de ne pas y arriver quand on voit que c'est evident sur le dessin ( comme tu me l'a fait remarqué ) !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités