Fcts réelles

[fight]

Bonsoir tlm ,

j'aimerais bien que vous me donnez des indications pour ces 2 exos sur les fcts réelles:

I) soit f: R--R une fct bornée.
On note E={g:R--R croissante tq g<=f} et pr x£R f'(x)=sup{g(x) tq g£E}
1)mq que f'£ E
2) on suppose que f est continue.mq f' est aussi continue.
S'il existe un point x0 £ R tq lim, qd x--x0-,f'(x)
II) soit f:[a,b]--R monotone. pr x£]a,b[ on pose d(x)=|lim, qd y--x-,f(y) 1)pr n£N* , mq En={x£]a,b[ tq d(x)>1/n} est fini.
2) En déduire que l'ens des points de discontinuité de f est au plus dénombrable.

je n'arrive plus à commencer aucun de ces 2 exos :triste: j'aimerais juste qqs indications ..

Merci bcp

[fight]

Personne pour m'aider? :triste:

[Nightmare]

Bonsoir,

tu n'arrives pas même à faire la question 1) du premier exo?

[fight]

en fait je ne suis pas sure , voilà ce que j'ai fait :
on a f bornée dc existe M>0 tq qq soit x£R |f(x)|soit A={g(x),g£E} on a E n'est pas vide (puisque f est bornée) dc A ne l'est pas également. et on a A est une partie de R majorée par M , donc ABS nous donne l'existence de supA=f'(x) .
me reste à montrer que supA £ E

est-ce juste ce que j'ai fait déjà ?

[fight]

euh je crois que j'ai rien montré là l'existence de supA est donné par l'énoncé :mur:

[fight]

svp , je demande pas des réponses mais juste des pistes . C'est pour préparer mon controle de demain et j'avoues que j'ai déjà bcp de retard :cry:

[fight]

bon voilà je poursuis ce monologue espèrant que qqn réagira...
pour 2ème exo :
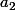
1) on considère l'application : qui à 1 associe et à 2 associe ..., n associe
tq et
mq f est inj:
soit ] tq soit tq
on a f est monotone , quitte à considérer -f , on suppose que f est croissante donc
l'unicité de la limite nous donne bien p=m , d'ou l'injectivité.
mq g est surj:
on a d(x)>0 , la propriété d'archimède nous donne l'existence de tq
d'ou la bijectivité de g ie En et [1,n] sont équipotent.

est-ce juste?

[fight]

:triste: ?!