Fction valeur abs

[guigui777]

Voilà je dois étudier la fonction valeur absolue de x élevée à une puissance a, avec a>1;
Ma question est comment montrer que c'est C1 sur R.... parce que pour moi ca bug en 0.... alors dans le corrigé ils disent que le Thm des acc finis permet de conclure quand à la dérivabilité de ma fonction en 0, j'vois pas trop pourquoi...? Et au passage, ce thm est-il souvent utilisé pour démontrer ce genre de chose, car moi c'est la première fois que je dois l'utiliser pour montrer la dérivabilité... d'habitude c'est une hypothèse :hum:
merci de votre aide!!

[nuage]

Salut,
une démonstration directe :
soit

car

[Lierre Aeripz]

On pose
Il est clair que f est dérivable sur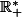 et sur .
Il manque la dérivabilité en zéro. Il suffit d'appliquer la définition.
On regarde la limite .
On trouve (vérifie-le) qu'elle vaut zéro. On en déduit que f est dérivable en zéro de dérivée zéro. Il suffit alors de vérifier la continuité de la dérivée.

Pour faire plus court, il y a le théorème de prolongement :
Pour continue et 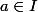, où I est un intervalle ouvert de . Si l'on suppose que f 'est sur I\{a} et que , alors f est sur I. En particulier,

[Amokrane]

oop dsl , j'ai fais une fausse manip et en + rien à dire vous pouvez effacer ce message :)