Fct kieme derivable..!!!

[mostdu95]

bonsoir
soit l'ensemble des fonctions f de R ds R DEFINIES par :
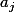et 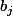st des reels et les elmts de st les polynomes de degre inferieur ou egale a n
Montrer que pour tout k ds N, la derivee K ième de f est dans T_n
j'ai choisi de faire un raisonnement par recurrence donc j'ai suppose que c'est vrai au rong n-1 mais j'arrive pas a montrer que c'est vrai au rong n
aidez moi s'il vous plait et si vous avez d'autres methodes n'esitez pas a me les montrer
et merci d'avance

[tito]

bonjour, on ne pourrait pas calculer de façon explicite la dérivé k-iéme de f et montrer qu'elle s'écrit bien comme un élément de Tn ?

[mostdu95]

d'abord mersi pour votre reponce tito;
j'ai deja ecris cela mais je sais pas la calcule plus precisement

[tito]

bonjour,

tu peut distiguer 2 cas celui ou k = 2p et k = 2p+1

pour k = 2p on a : D(2p)(cos(jx)) = j^(2p).((-1)^p).cos(j.x)
D(2p)(sin(jx))= j^(2p).((-1)^p).sin(j.x)

donc D(2p)(f(x))= somme( Rj.cos(j.x) + Tj. sin(j.x) , j=0......n)
est bien un élément de Tn avec Rj = aj.(j^(2p)).((-1)^p) et Tj =........
qui sont bien des réels.
on fait la méme chose avec k=2p+1 ( on obtiendra un sin à la place du cos et un cos à la place du sin ) mais cela sera tj un élmts de Tn
bien sur tous les résultats sont à vérifier

[xyz1975]

soit l'ensemble des fonctions f de R ds R DEFINIES par :

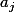
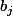
et st des reels et les elmts de st les polynomes de degre inferieur ou egale a n

C'est quoi Tn en juste?
La dérivée k-ième de cos(x) est cos(x+kpi/2). De même pour sin.

[mostdu95]

pourquoi j^(2p) et (-1)^p ; on peut pas faire trainer 2p comme ça ,c'est pas un exposant le nbre de drivee.dc si je comprend bien vous supposer ds un premier tps que le nbre de fois où vs derivez f est pair mais je ne suis pas d'accord avec la formule que vous trouver ou du moins je ne l'ai pas comprise .....

[mostdu95]

C'est quoi Tn en juste?
La dérivée k-ième de cos(x) est cos(x+kpi/2). De même pour sin.

st les polynomes trigonometrique de degre inferieur ou egale a n et c'est l'ensemble des fct de la forme de f

[mostdu95]

ahhhhhhhhhhhhhhhhhhh c'est bon j'ai compris merci beaucoup TITO youpii

[tito]

:p de rien et bonne chance !

[mostdu95]

j'ai une autre question
si f s'annule 2n+1 fois points distincts de l'interv [a,a+2pi] avec a appartient R .comment je peux montrer que f' s'annule en 2n+1 points distincts de cet intervalle
et merci encore

[mostdu95]

j'ai une autre question
si f s'annule 2n+1 fois points distincts de l'interv [a,a+2pi] avec a appartient R .comment je peux montrer que f' s'annule en 2n+1 points distincts de cet intervalle
et merci encore

[bitonio]

j'ai une autre question
si f s'annule 2n+1 fois points distincts de l'interv [a,a+2pi] avec a appartient R .comment je peux montrer que f' s'annule en 2n+1 points distincts de cet intervalle
et merci encore

Salut,
il faut appliquer Rolle assez judicieusement.

Ps: A noter (pour info car pas utilie pour ec que tu cherches à montrer) que si f s'annule 2n+1 fois sur [a;a+2[, alors f est identiquement nulle (il faut considérer un polynôme trigonométrique)

[tito]

bonjour, f est une fonction quelconque ?

[bitonio]

bonjour, f est une fonction quelconque ?

Bonjour,
il est d'usage de lire le début du post avant d'intervenir...

[mostdu95]

bonjour, f est une fonction quelconque ?

nn f c'est la fonction de depart:

[tito]

bonjour, alors ya un truc que je comprend pas d'aprés la déf. de départ f est une fonction polynomiale de R dans R de degrés inférieur ou égal à n comment peut-elle avoir 2n+1 racines ?

[mostdu95]

c'est les elements de T-n qui sont de deg <=n et j'ai juste dis que t_n est l'ensemble des polynomes trigo de la forme de f ça sous entends que f peut etre de dgre > n,
en fait j'ai essayé de resume mon ennonce c'est pour ça que g dis a la fois que tn etait ens des poly trig < n ....desolé

[nuage]

Salut,

j'ai une autre question
si f s'annule 2n+1 fois points distincts de l'interv [a,a+2pi] avec a appartient R .comment je peux montrer que f' s'annule en 2n+1 points distincts de cet intervalle
et merci encore

tu peux pas car c'est faux.
A titre d'exemple prendre a=0 et f=sin

[mostdu95]

c'est un sujet de concour donc je pense pas quia une erreure.....!!!!!!!!!!!!!!!!
de toute façon la question c'est de mq SI f s'annule en 2n+1 points distinct de l'intervalle comment peut on montrer que la derivee l'est aussi

[nuage]

Salut,
Il faut ouvrir l'intervalle [a; a+2 pi] au moins d'un côté.
Ensuite si f est dérivable sur [a;b] et f(a)=f(b) alors il existe c dans [a;b] tel que f'(c)=0 (théorème de Rolle).