Familles libres

[rifly01]

Bonjour,

Quelqu'un pourrait me dire si ce que j'ai fait est juste ?

[CENTER] [/CENTER]

1) (Q', Q', Q'', Q''') n'est pas une famille libre car Q''' = 0.

2) Soient , , ,

Soient tel que
Et donc :

D'ou Il s'agit donc d'une famille libre.
On peut prendre a=b=c=d=1 ... et je pense que ca marche aussi x^3, vu que la dérivée tièrce n'est pas nulle.

Est-ce correct, Je n'ai pas très bien assimiler ce chapitre. Merci d'avance

[Nightmare]

Bonsoir

Et la suite ?

[Nightmare]

Je ne comprends pas, si tu réponds à la 1) que viens faire les a, b, c et d alors que ton polynômes est posé comme égal à X^3-3X+1 à la base.

Si tu réponds à la 2), où est l'exemple?

[rifly01]

Pardon, j'ai poster avant de terminer mon blabla... : le a,b,c,d c'est pour le deux.

[Nightmare]

La conclusion lambda1=lambda2=....=0 est fausse, ce n'est pas parce que ab=0 que b est forcément nul, ça peut être a qui l'est.

[rifly01]

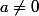
mais par hypothèse , plus encore

[Nightmare]

Et pourquoi b, c et d doivent-ils être non nuls?

Et puis il suffit de prendre b=3 et a=-1 pour obtenir un Lambda2 non nul.

Ta démonstration ne tient pas debout. De toute façon tu as démontré quoi? Que quelque soit le polynôme de degré 3 la famille (P,P',P'',P''') est libre, or dans le premier exercice on te donne un polynôme Q de degré 3 tel que la famille (Q,Q',Q'',Q''') est liée, c'est quand même bizarre !

[rifly01]

Zut alors, je recomence ... et je poste :)

[rifly01]

Soit ,
a étant un réel quelconque distinct de zero.

alors est une famille libre

Juste ?

ah, et pour la 1) c'est bon ?

[Nightmare]

Oui c'est juste.

:happy3:

[rifly01]

Merci bcq, je vais certainement continuer à poster ... :) parce que je trouve des réponses par ici lol