Familles libres

par **Anonyme** » 13 Fév 2010, 16:00

Bonjour, pourriez-vous me donner la solution ou même des pistes pour cet exercice svp ?

Si (u1,u2,_,un) libre dans C alors (Re(u1),_,Re(un)) et (Im(u1),_,Im(un)) libres dans R.

Merci d'avance

par **Nightmare** » 13 Fév 2010, 16:14

Salut,

tu as essayé ? Rien de difficile, il suffit juste de connaitre les définitions et de les appliquer !

par **Anonyme** » 14 Fév 2010, 23:12

Oui oui j'ai essayé ^^'

par **Sylviel** » 15 Fév 2010, 11:10

Quel est la caractérisation la plus simple d'une famille libre ?

par **Anonyme** » 15 Fév 2010, 12:46

Soit lambda1, lambda2... tq lambda1 re(u1)+...=0 -> tous sont nuls.

par **Anonyme** » 18 Fév 2010, 13:23

Personne n'a d'idée ?

par **Anonyme** » 29 Aoû 2010, 23:05

Up (tardif)

par **MacManus** » 29 Aoû 2010, 23:28

Bonsoir.

Si l'on suppose que la famille

est libre, alors .... donc...

par **Doraki** » 30 Aoû 2010, 08:33

Vous saviez qu'il existe des complexes non nuls dont la partie réelle est nulle ?

par **Anonyme** » 30 Aoû 2010, 09:24

Je vous assure que j'ai essayé hein, et que ce n'est pas un exo trivial (à moins que je n'y sois pas du tout)...

par **Doraki** » 30 Aoû 2010, 09:28

Tu n'y es pas du tout : C'est un exo faux.

par **benekire2** » 30 Aoû 2010, 09:36

Salut Arnaud,

Déjà quand tu dit (u1,u2,...,un) sont libres dans C, tu veut dire que (u1,u2,...,un) est une famille libre de C en tant que C-espace vectoriel ?

Dans ce cas, ta famille n'a qu'un seul vecteur non nul . Et donc, dans ce cas, le résultat que tu veut montrer est faux, seulement l'un sera juste.

Cela dit soit c'est moi qui fait fausse route, soit il manque des hypothèses,

par **euler21** » 30 Aoû 2010, 12:19

Salut
En fait il y a un résultat sur les espaces vectoriels qui dit qu'un C espace vectoriel de dimension n peut être considéré comme un R espace vectoriel de dimension 2n. Je pense que c'est ça l'objectif de ta question. Seulement il va falloir bien formuler pour y arriver.

par **euler21** » 30 Aoû 2010, 12:24

plus précisément si

libre dans E en tant que C ev
alors

est libre dans E en tant que R ev.
Je pense c'est ça le résultat qu'il faut démontrer

par **Finrod** » 30 Aoû 2010, 13:02

Pas besoin d'aller chercher aussi loin euler.

D'ailleurs ta famille de vecteurs est dans

donc dans

.

(cela dit ta famille sera certainement R-libre et non C-libre)

Comme l'a fait remarqué Doraki, en passant à R, il peut y avoir une partie réelle ou imaginaire nulle.

Cela dit, si l'on regarde le vecteur de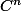

comme un vecteur de

, là oui, il sera R-libre.

Par exemple, pour un seul vecteur, libre signifie non nul et il est clair que z non nul dans C si et seulement si (Re(z),Im(z)) est un vecteur non nul de R².

Bien entendu, cela n'est pas équivalent à (Re(z),0) ; (0,Im(z)) libre.

par **Anonyme** » 31 Aoû 2010, 07:33

Oups, autant pour moi, j'ai oublié de préciser que les ui sont des fonctions.

par **Anonyme** » 31 Aoû 2010, 21:42

Up (caractères)

par **Doraki** » 31 Aoû 2010, 21:54

Bah comme on te l'a dit, tel quel, l'exo est faux :

La fonction constante qui donne i est une famille libre à 1 élément.
Sa partie réelle, la fonction constante qui donne 0, n'est pas une famille libre à 1 élément.

par **Anonyme** » 01 Sep 2010, 09:59

Ah bah oui... mmm merci et désolé....

Familles libres

Familles libres

Qui est en ligne