Famille liée de vecteurs

[georgess]

Bonsoir , j'ai l'exercice suivant : Montrer qu'une famille de vecteurs est liée si et seulement si l'un des vecteurs est combinaison linéaire des autres .

Voici la démonstration que je propose :

Soit V {v1,v2,...,vn} une famille de vecteurs . Soient a1,a2,...,ai des scalaires appartenant à R .

Si la famille de vecteurs est liée on peut écrire que :

a1v1 + a2v2 + ...+ aivn = b , b étant un nombre réel différent de 0 .

Si vn est combinaison linéaire des autres cela se note : vn = a1v1 + a2v2 + ...+ajvm .

Ca donne :

a1v1 + a2v2 +...+a1v1+a2v2 = b

a1 et a2...sont obligatoirement différent de 0 donc la famille est liée . Que pensez vous de ma démonstration ?

merci

[kazeriahm]

:

Soit V {v1,v2,...,vn} une famille de vecteurs . Soient a1,a2,...,ai des scalaires appartenant à R .

Si la famille de vecteurs est liée on peut écrire que :

a1v1 + a2v2 + ...+ aivn = b , b étant un nombre réel différent de 0 .

hum hum

intéressant

[georgess]

non b étant un réel tout court je me suis trompé , sinon ma démonstration est elle juste ?

[leon1789]

disons qu'il y a un problème à ce niveau :

Si b est un réel, les sont de quel type ? et les ??

[georgess]

les ai ce sont des réels et les vi des vecteurs

[bitonio]

Il y a un problème d'homogénéité.. Un vecteur ne peut pas être égal à un réél.

Sinon ta démo me parrait fausse:

je verrai plus: car la famille est liée. En considérant tel que est non nul, on peut isoler d'un coté quitte à diviser tout le monde par supposé non nul

[georgess]

j'ai pas dit le contraire dans ma démonstration je pense...

[bitonio]

Relis mon post...

[leon1789]

les ce sont des réels et les des vecteurs

ok, alors de quel type est ?

[georgess]

oui ce sont des réels effectivement , mais alors tu peux m'aider dans ma démonstration stp ?

[georgess]

j'aimerais rester sur le début de ma démonstration qui me semble juste s'il te plait

[leon1789]

C'est mal parti, car les sont bien des réels, les des vecteurs, et donc un vecteur aussi !!!

[bitonio]

j'aimerais rester sur le début de ma démonstration qui me semble juste s'il te plait

Oublie ta démo elle est completement fausse! Lis plutôt ce qu'on te poste au lieu de t'entêter!!!

[georgess]

tu postes des formules toutes faites sans rien expliquer clairement donc ça ne m'avance pas bcp tu sais..

[fatal_error]

Bonjour,

a_1v_1 + a_2v_2 + ...+ a_n v_n un vecteur aussi !!!

Ce qu'a dit Leon1789 resume lerreur que tu as faite. Un scalaire fois un vecteur, ca donne un vecteur, est un vecteur, ca peut pas etre ton réel b.

[BertrandR]

Je suis d'accord avec les posteurs, ta démonstration est completement fausse... Tout simplement en ce qui concerne les lois d'espace vectoriels, à savoir une LCI (+) et une LCE dans les corps des scalaires(.). Puisque tu ne travaille pas sur des forme linéaires ou autre, tu ne peux pas faire une operation avec des vecteurs et des scalaires en te retrouvant dans le corps des scalaires. D'ailleurs attention, le 0 que l'on écrit dans ces démonstrations est le vecteur nul et pas le 0 du corps des scalaires.Je te propose la suivante, et je te conseille de l'associer avec ton cours sans lequel tu n'iras pas loin :

S'il existe des scalaires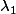 , ..., 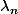tels que , alors on a
, et par suite la famille () est liée.

Si la famille () est liée, alors il existe non tous nuls tels que :

Si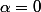 alors


avec les lambda i non tous nuls ce qui est absurde car la famille des x_i est libre. On en déduit alpha different de 0 et don :

[leon1789]

Je peux me faire un peu de pub ? :ptdr:
Voir le dernier paragraphe, tout à fait en bas du message
http://www.maths-forum.com/showpost.php?p=320267&postcount=30
Si vous voulez, vous pouvez y laisser vos commentaires :we: