Bonjour,
Je galère depuis ce matin sur une notion que je ne comprends pas, la voici :
Le but du paragraphe est de construire un faisceau d'anneaux

sur l'espace topologique
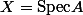
avec

un anneau commutatif tel que pour tout

, la tige
_{ \rho } $)
soit le localisé

de

par rapport à la partie multiplicative

, et

: la restriction du faisceau

à l'ouvert
 = \{ \rho \in \mathrm{Spec} A \ : \ f \not \in \rho \} $)
soit isomorphe à

avec
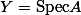
. On rappelle que

est le localisé de

par rapport à la partie multiplicative

.
Voici le passage que je ne comprends pas :
On va d'abord, définir l'anneau
 ) $)
et les applications de restrictions
 ) \to \mathcal{O}_{X} (D(g)) $)
quand
 \subset D(f) $)
. On pose :
 ) = A_f $)
.
Pourquoi, si
 \subset D(f) $)
, alors, cela signifie que
} $)
( i.e :
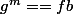
), et donc

est inversible dans

, et on obtient un homomorphisme de restriction

provenant de la définition de la localisation ( cela revient à envoyer

sur

)
Je ne saisis pas bien ce passage dans ma tête.
Merci pour votre aide.
P.S : Écrivez moi la réponse en détail svp, car je ne comprends pas bien ce qui est écrit là.
