Factorisation polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
elemarre
- Membre Naturel
- Messages: 39
- Enregistré le: 30 Déc 2014, 14:35
-
 par elemarre » 10 Jan 2015, 10:05
par elemarre » 10 Jan 2015, 10:05
Bonjour je voulais savoir lorsque l'on demande de faire une factorisation dans R(x) de par exemple:
5*z^3= -1, doit-on résoudre en cherchant les racines de z^3= -1/5 ou juste z^3=-1 et mettre dans la décomposition en facteurs irréductibles de R(x) le 5 en facteur?
Merci

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 10 Jan 2015, 10:16
par fatal_error » 10 Jan 2015, 10:16
ben tu fais comme tu veux, mais le but c'est que une fois que tu as trouvé tes z,
ils satisfassent ton égalité...
à priori, t'as quand meme envie de passer en notation exponentielle.
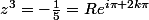
avec
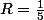
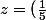^{\frac13}e^{ i\frac{(2k+1)\pi}{3}})
, pour k=0,1 ou 2
la vie est une fête

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Jan 2015, 16:23
par Carpate » 10 Jan 2015, 16:23
elemarre a écrit:Bonjour je voulais savoir lorsque l'on demande de faire une factorisation dans R(x) de par exemple:
5*z^3= -1, doit-on résoudre en cherchant les racines de z^3= -1/5 ou juste z^3=-1 et mettre dans la décomposition en facteurs irréductibles de R(x) le 5 en facteur?
Merci
^3+1^3=(\sqrt[3]{5}z+1)[(\sqrt[3]{5}z)^2-\sqrt[3]{5}z+1])
-
elemarre
- Membre Naturel
- Messages: 39
- Enregistré le: 30 Déc 2014, 14:35
-
 par elemarre » 10 Jan 2015, 18:19
par elemarre » 10 Jan 2015, 18:19
Merci bien pour vos réponses
-
mathelot
 par mathelot » 10 Jan 2015, 20:11
par mathelot » 10 Jan 2015, 20:11
elemarre a écrit:Bonjour je voulais savoir lorsque l'on demande de faire une factorisation dans R(x) de par exemple:
5*z^3= -1, doit-on résoudre en cherchant les racines de z^3= -1/5
Merci
.................
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
