Factorisation polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 17:35
par pantin » 01 Nov 2012, 17:35
Salut,
j'aurais besoin d'aide pour un exercice de factorisation de pôlynome dont je n'ai pas réussi à faire les derniers exemples.

Merci pour votre aide

-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 01 Nov 2012, 17:39
par Arnaud-29-31 » 01 Nov 2012, 17:39
Bonjour,
Tu as fais quoi déjà ?
-
homeya
- Membre Relatif
- Messages: 218
- Enregistré le: 05 Mar 2012, 10:20
-
 par homeya » 01 Nov 2012, 17:42
par homeya » 01 Nov 2012, 17:42
Bonjour,
Pour le premier polynôme, on peut poser X = x^4 pour se ramener au second degré.
Pour le second, on peut factoriser par x^2+1 et on retrouve une expression bicarrée.
Cordialement.
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 17:46
par pantin » 01 Nov 2012, 17:46
Salut, j'ai déjà, fait le reste de mon exercice ou une simple division euclidienne suffisait mais là je bloque.
pour le second j'ai réussi sur R et j'obtient:
(x^4-x^2+1))
merci

-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 17:47
par pantin » 01 Nov 2012, 17:47
je vais faire le premier avec votre méthode merci .
-
homeya
- Membre Relatif
- Messages: 218
- Enregistré le: 05 Mar 2012, 10:20
-
 par homeya » 01 Nov 2012, 17:48
par homeya » 01 Nov 2012, 17:48
Pour le dernier, 2 + i est racine "évidente" (en fait plutôt semi-évidente quévidente :happy2: ) ...
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 01 Nov 2012, 17:50
par Arnaud-29-31 » 01 Nov 2012, 17:50
C'est juste pour la factorisation sur

mais on peut faire mieux. Pour celle sur

, as tu entendu parler de racine
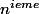
de l'unité ?
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 17:53
par pantin » 01 Nov 2012, 17:53
Pour la première je trouve dans un premier temps avec l'équation du second degrès e^(2ipi/3) et e^(-2ipi/3) et après je dois faire quoi svp ?
=> Arnaud oui j'ai déjà fait les racine n-ième de l'unité
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 17:55
par pantin » 01 Nov 2012, 17:55
pour le 2+i de la dernière, même avec un logiciel de calcul formel je ne l'ai pas trouvée :p
-
homeya
- Membre Relatif
- Messages: 218
- Enregistré le: 05 Mar 2012, 10:20
-
 par homeya » 01 Nov 2012, 17:56
par homeya » 01 Nov 2012, 17:56
Il faut ensuite revenir à x (ou z) en résolvant z^4 = e^(2ipi/3) et z^4 = e^(-2ipi/3) ...
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 17:58
par pantin » 01 Nov 2012, 17:58
ahh ok merci, je sais comment conclure pour la 1 maintenant
-
homeya
- Membre Relatif
- Messages: 218
- Enregistré le: 05 Mar 2012, 10:20
-
 par homeya » 01 Nov 2012, 17:59
par homeya » 01 Nov 2012, 17:59
@Pantin: pour 2+i, j'ai utilisé Maxima qui m'a donné cette réponse ... oui je sais, je triche un peu :ptdr:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 01 Nov 2012, 18:00
par Arnaud-29-31 » 01 Nov 2012, 18:00
Lorsque tu dois factoriser sur R et C le mieux est de commencer par C. Si c'est bien fait, on fait apparaitre les racines à regrouper pour obtenir la factorisation sur R et cela permet d'obtenir la meilleur factorisation possible : le
.(x^4-x^2+1))
que tu proposes peut être amélioré.
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 18:01
par pantin » 01 Nov 2012, 18:01
moi j'utilise wolframalpha mais il m'a donné une forme étrange
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 18:02
par pantin » 01 Nov 2012, 18:02
Arnaud-29-31 a écrit:Lorsque tu dois factoriser sur R et C le mieux est de commencer par C. Si c'est bien fait, on fait apparaitre les racines à regrouper pour obtenir la factorisation sur R et cela permet d'obtenir la meilleur factorisation possible : le
.(x^4-x^2+1))
que tu proposes peut être amélioré.
on peut améliorer le terme de droite en posant X=x^2 il me semble
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 01 Nov 2012, 18:08
par Arnaud-29-31 » 01 Nov 2012, 18:08
Oui voila.
Sinon on pouvait passer par C même si ce n'est pas demandé et revenir à R en regroupant les racine conjuguées.
Sinon pour le 1 une fois que l'on a posé

on a
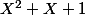
donc les racines sont j et son conjugué (racines cubique de 1).
Pour le dernier si c'est donné par l'énoncé de l'on a une racine triple alors ca simplifie pas mal de choses.
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 18:10
par pantin » 01 Nov 2012, 18:10
Oui pour le dernier c'est donné par l'énoncé
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 01 Nov 2012, 18:13
par Arnaud-29-31 » 01 Nov 2012, 18:13
On peut donc poser
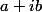
cette racine. On sait que notre expression se factorise
^3)
, en développant et en identifiant on trouve bien a = 2 et b = 1.
-
pantin
- Membre Naturel
- Messages: 51
- Enregistré le: 18 Nov 2011, 17:39
-
 par pantin » 01 Nov 2012, 18:16
par pantin » 01 Nov 2012, 18:16
Arnaud-29-31 a écrit:On peut donc poser
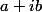
cette racine. On sait que notre expression se factorise
^3)
, en développant et en identifiant on trouve bien a = 2 et b = 1.
Après je sais faire normalement car j'ai un exemple de cours qui ressemble à celà.
Et bien je vous dit un grand merci à tous pour votre aide et pour vos explication :we: (...et pour le logiciel)
Bonne fin de soirée à vous tous
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 01 Nov 2012, 19:38
par fibonacci » 01 Nov 2012, 19:38
Bonsoir;
puisqu'il y a une racine multiple d'ordre 3
il suffit de dériver 2 fois trouver la valeur qui annule la dérivée seconde, et l'on a
)
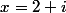
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités


que tu proposes peut être amélioré.
cette racine. On sait que notre expression se factorise
, en développant et en identifiant on trouve bien a = 2 et b = 1.