Factorisation polynome

par **franz00** » 03 Nov 2010, 02:08

bonjour a tous,

jai besoin d'aide pour factoriser dans C puis dans R le polynome :

P(X) = X^8 + X^4 +1

Merci de votre aide

par **Harchy** » 03 Nov 2010, 02:20

Tu peux poser Y=X^4 et factoriser le polynôme en Y

par **franz00** » 03 Nov 2010, 02:30

ok je vais essayer ca merci

par **franz00** » 03 Nov 2010, 02:41

J'ai Y² + Y +1 = 0

2 racines complexes (-1 +/- i * racine de 3 )/2 et comme Y = X^4 va falloir que je calcule la racine 4e de ca c a dire (x+iy) ^4 = Y1,Y2 donc ca revient a resoudre 2 fois de suite lequation

(x+iy)² = Y1,Y2

c'est bien ca ?

par **Harchy** » 03 Nov 2010, 02:45

C'est ça.
On note ces racines aussi j et j².

Je pense que la forme exponentielle est celle qui permet le mieux de résoudre Z^4=c ou c est un complexe donné

par **Ericovitchi** » 03 Nov 2010, 09:09

Et donc tu trouves

c'est ça ?

par **Ben314** » 03 Nov 2010, 10:15

Il y a aussi "l'astuce" consistant à voir que :

lorsque

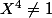
(série géométrique)
donc les racines de P sont les 8 racines 12-ièmes de l'unité qui ne sont pas racines 4-ièmes de l'unité.

Factorisation polynome

factorisation polynome

Qui est en ligne