Bonjour à tous.
J'ai une fraction qui utilise différentes puissances d'une variable et j'aimerais pouvoir ne faire apparaître qu'une seule fois la variable.
Ma fraction :
(a-x)/sqrt (x/n)
J'aimerais ne faire apparaître qu'une seule fois le x.
Factorisation fraction.
12 messages
- Page 1 sur 1
Re: Factorisation fraction.
On ne peut pas toujours.
dans x²+2x+1, on est obligé de garder le x².
avec les racines c'est pareil (sqrt(x), c'est x^(1/2))
d'ailleurs, une méthode de résolution de (a-x)/sqrt (x/n) =b est d'élever les deux membres au carré, la racine disparaît, un x² apparaît, on résout et on ne garde que les solution compatibles avec l'équation de départ.
dans x²+2x+1, on est obligé de garder le x².
avec les racines c'est pareil (sqrt(x), c'est x^(1/2))
d'ailleurs, une méthode de résolution de (a-x)/sqrt (x/n) =b est d'élever les deux membres au carré, la racine disparaît, un x² apparaît, on résout et on ne garde que les solution compatibles avec l'équation de départ.
Re: Factorisation fraction.
En réalité, il s'agit de trouver un intervalle de confiance 1-alpha sur
(ê - e)/sqrt(e/n) -> N(0,1) où ê est un estimateur du paramètre e.
On a donc P( u(alpha/2) <= (ê - e)/sqrt(e/n) <= u(1 - (alpha/2) ) ) = 1- alpha , ou u(t) est le fractile d'ordre t de la loi Normale.
Et on veut donc finir avec un intervalle de confiance
P(a <= e <= b) = 1-alpha
Avec a et b qui dépendent évidemment de ê, de n et des fractiles de la loi Normale.
(ê - e)/sqrt(e/n) -> N(0,1) où ê est un estimateur du paramètre e.
On a donc P( u(alpha/2) <= (ê - e)/sqrt(e/n) <= u(1 - (alpha/2) ) ) = 1- alpha , ou u(t) est le fractile d'ordre t de la loi Normale.
Et on veut donc finir avec un intervalle de confiance
P(a <= e <= b) = 1-alpha
Avec a et b qui dépendent évidemment de ê, de n et des fractiles de la loi Normale.
Modifié en dernier par PaulOchon le 06 Avr 2017, 16:24, modifié 1 fois.
Re: Factorisation fraction.
salut
déjà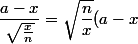) ...
...
déjà
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Factorisation fraction.
Salut,
Je comprend pas grand chose à la question, mais ça donne vaguement l'impression que, pour connus, tu cherche à résoudre un truc du style
connus, tu cherche à résoudre un truc du style  .
.
Si c'est bien le cas, ben chacune des inégalité, c'est une bête inéquation du second degré en et il n'est (heureusement...) nul besoin de "faire apparaître qu'une seule fois le x" pour résoudre ce type de truc.
et il n'est (heureusement...) nul besoin de "faire apparaître qu'une seule fois le x" pour résoudre ce type de truc.
Je comprend pas grand chose à la question, mais ça donne vaguement l'impression que, pour
Si c'est bien le cas, ben chacune des inégalité, c'est une bête inéquation du second degré en
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Factorisation fraction.
PaulOchon a écrit:
tu peux étudier la fonction
Exemple avec n=100 et a=3:
- Fichiers joints
-
- fig1.jpg (15.79 Kio) Vu 451 fois
Re: Factorisation fraction.
Je ne connais pas n et a.
Ce sont des résultats théoriques pas d'application numérique.
En plus a est une statistique sur un échantillon de taille n.
Ce sont des résultats théoriques pas d'application numérique.
En plus a est une statistique sur un échantillon de taille n.
Re: Factorisation fraction.
a c'est une statistique donc elle peut prendre n'importe qu'elle valeur. C'est un estimateur du parametre x (en général noté  ) d'une loi de poisson
) d'une loi de poisson
Re: Factorisation fraction.
On va pas non plus passer 15 jours sur une malheureuse équation du second degré...
\!\leq\! u\ \Leftrightarrow\ (a\!-\!x)^2\!\leq\!u^2\frac{x}{n}\ \Leftrightarrow\ x^2\!-\!(2a\!+\!\frac{u^2}{n})x\!+\!a^2\!\!\leq\!0)
^2\!\!-4a^2\!=\!\frac{u^2}{n}(4a\!+\!\frac{u^2}{n})\,>0)
Et l'ensemble des solutions de l'inéquation est
Et l'ensemble des solutions de l'inéquation est
Si tu prend une loi de poisson avec un paramètre négatif, ben ça va un tout petit peu te faire... des proba négatives...PaulOchon a écrit:a c'est une statistique donc elle peut prendre n'importe qu'elle valeur. C'est un estimateur du parametre x (en général noté) d'une loi de poisson
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
