Facteurs premiers.

[yos]

Bonsoir à tous.

Y aurait-il une bonne âme sachant parler aux ordinateurs, qui me trouverait un entier t tel que N= t²+3t+9 possède au moins 9 facteurs premiers distincts et autres que 3.
Pas trop grand quand même le N.
De plus pour chacun de ces 9 diviseurs premiers p, il faudrait que p^3 ne divise pas t²+3t+9, mais je pense qu'avec un minimum de bol cette dernière condition devrait se présenter toute seule.

Reconnaissance éternelle

[memphisto]

salut, je sais parler aux ordinateurs, mais je suis dans un cyber, je n'ai donc pas mes outils de développement avec moi, et chez moi je n'ai pas encore internet :/
cependant, comme ton entier N ne doit pas contenir le fateur premier 3, il résulte que la classe de N modulo 3, s'écrit t² dans ,
donc différente de la classe de 0 ou la classe de -1.
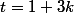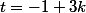Donc ou , pour un certain entier k.
Donc ou pour un certain entier k.

Cela devrait déja aider a supprimer pas mal de possiblités.

[memphisto]

bien sur, j'ai fais cela a l'arrache; ce n'est qu'une implication, et pas une équivalence. En tout cas il n'y a aucune raison.
Mais comme je dois y aller, je réfléchirait au problème chez moi.
aller a plus.

[yos]

Merci d'avoir regardé mon problème.
Je me suis mal exprimé :
N peut être divisible par 3 mais il faut qu'il ait 9 diviseurs premiers (au moins) autres que 3. De même il peut être divisible par un p^3 mais alors ce p là ne sera pas pris en compte dans les 9 nécessaires.
Ta remarque est intéressante car tant qu'à faire, autant que 3 n'y figure pas (ça peut diminuer la taille du nombre N).
Je me demande si on ne peut pas se contenter de remplacer t par un nombre au hasard (disons à 5 chiffres) et factoriser N, mais pour ça, il me faudrait un factoriseur. Je n'en ai pas. Peut-être qu'il y en a sur le net?

[memphisto]

tout a fait, il y a la librairie GP/pari, disponible ici:
http://perso.wanadoo.fr/jean-paul.davalan/liens/liens_softedu.html
au lien:
ftp://megrez.math.u-bordeaux.fr/pub/pari/
aller dans la section windows, et télécharger la version 2.2.12 au lien:
ftp://megrez.math.u-bordeaux.fr/pub/pari/windows/Pari-2-2-12.exe

Les manuels d'utilisation, FAQ, etc, se trouvent au lien:
http://megrez.math.u-bordeaux.fr/ mais aussi, l'aide est installée en même temps que l'application.

L'install se fait toute seule, et il suffit de lancer gp.exe.
Pour l'aide, taper "?"

La section de l'aide qui t'intéresse se trouve à la section "?4"

C'est en fait la fonction factor(). Il suffit de taper "? factor" pour avoir l'aide sur la fonction.

Cette librairie a été développée par l'équipe du professeur Henri Cohen à l'univerité de bordeau, et est très performante. Chacune de ses mises à jour utilisent les derniers développements de la géométrie algébrique, et on peut même la recompiler a partir de ses sources en la "débridant". Elle peut alors factoriser les nombres utilisés dans les dernières spécifications des algos de chiffrement à clef publique RSA et DSA...pourvu que l'on ait la puissance de calcul adéquate :/

J'espère t'avoir aidé.
A bientot.

[yos]

Merci beaucoup. J'essaierai ça demain.

[memphisto]

Re,
donc autre chose:
si p est un diviseur de N (et on veut en trouver 9 comme cela), alors dans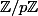 l'équation devient puisque la classe de N mod p est nulle. De plus, l'équation admet des solutions dans 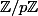ssi le polynome est factorisable dans en produits de facteurs linéaires . On récupères donc deux valeurs pour lesquelles l'équation s'annule: . Ces deux solutions donnent lieu à deux valeurs de t dans comprises entre 0 et p-1: 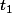et 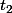, qui définissent deux classes modulo p: et , dont les éléments t vérifient la propriété: "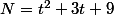 est divisible par p".

Il suffit donc de trouver 9 nombres premiers tels que soit dissocié dans , car alors par le théorème des restes chinois, on récupère un entier t vérifiant que N admet dans sa décomposition en facteurs premiers les 9 facteurs premiers .
Attention, on ne connais pas encore les puissances de ces 9 nombres premiers dans N. Il faudra les déterminer, pour ne pas prendre en compte ceux qui vérifient que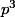 divise N.

Donc problème:

Trouver les nombres premiers p pour lesquels est dissocié dans .

remarque: dans , et donc également dans , pour tout premier p.

à suivre...

[memphisto]

Par exemple, notons notre polynome.
Alors dans , P est irréductible, alors que dans , P se factorise en ( modulo 7).

Donc tout N qui s'écrit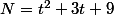 , avec t=-2+7k ou t=-1+7k, pour un certain entier k strictement positif, on a la propriété: "7 divise N". En effet:
et:
.


Avec la librairie GP/Pari:
tapez "pol= t^2 + 3*t + 9"
puis "polrootsmod(pol,5)" pour le factoriser modulo 5, ou
"polrootsmod(pol,7)" pour le factoriser modulo 7.

Dans le premier cas on obtient "[]~". Donc aucune factorisation.
Dans le second, on obtient "[Mod(5, 7), Mod(6, 7)]~", qui veut dire la classe de 5 modulo 7, et la classe de 6 modulo 7.
Donc modulo 7, .

Puis on continue:
"polrootsmod(pol,11)" nous montre que P est irréductible modulo 11,
mais "polrootsmod(pol,13)" fournit les solutions classe de 1 et classe de 9 modulo 13.

De cette manière, on trouve les nombres premiers:
7, 13, 19,.31, 37, 43, 61, 67, 73.
Pour chacun de ces 9 nombres premiers, on trouve les classes (je n'en prend qu' une par nombre premier sur les deux):
5+7k, 1+13k, 2+19k, 13+31k, 4+37k, 18+43k, 19+61k, 20+67k, 24+73k.

à suivre...

[yos]

Salut.
Je sais faire la partie théorique : j'avais déjà trouvé que les premiers 7,13,19,31,37,43,61,67 divisent N pour t de la forme respectivement :
7k-1 ou 7k- 2,
13k+1 ou 13k+9,
19k+2 ou 19k+14,
31k+13 ou 31k+15,
37k+4 ou 37k+30,
43k+18 ou 43k+22,
61k+19 ou 61k+39,
67k+20 ou 67k+44.

Via la loi de réciprocité quadratique, je sais que les autres plus petit que 67 ne peuvent diviser N. Je peux bien sûr en trouver un 9ème en deux minutes, mais je ne sais pas trop si huit peut suffire ou pas. En tout cas ce n'est pas le problème. Il est clair qu'il y en a une infinité et que le chinese remainder theorem permet de construire t tel que N possède un nombre arbitraire de diviseurs premiers. Cela dit, les solutions du problème sont modulo 7X13X19X31X37X43X61X67, ce qui est déjà gros. D'où ma demande d'un numéricien (par flemme je reconnais).

En tout cas merci pour ta référence à PARI que je connaissais mais que je n'avais pas téléchargé. Je viens de le faire et de tester la fonction factor sur ce problème : on voit qu'avec des t au hasard, c'est pas gagné!
Il faut que je m'entraîne à l'utiliser pour des groupes de classes ou de Galois. En tout cas on voit bien que c'est un produit universitaire : pas convivial du tout.

A bientôt et merci encore.

[memphisto]

voila, par le théorème chinois, on obtient: t=25285696305728+25442182561159k.
Pour k=0, on a: t=25285696305728
d'où:
N=639366437665582483934527177
est divisible par:
D= 25442182561159=7*13*19*31*37*43*61*67*73, et:
N/D=25130172544303.
De plus, N/D n'est divisible pas aucun des 9 nombres premiers 7, 13, 19,.31, 37, 43, 61, 67, 73.
Donc les puissances de ces nombres premiers dans N sont toutes 1.

Une réponse au problème est donc N=639366437665582483934527177.


Ceci dit, il me semble qu'il y a une règle pour produire les nombres premiers qui vérifient la relation que l'on veut, alors que là je me suis aidé de pari pour factoriser les polynomes dans les corps premiers. Cette démarche est donc ad hoc, donc pas forcément satisfaisante au point de vue théorique.
Mais elle fournit une solution :/

[yos]

voila, par le théorème chinois, on obtient: t=25285696305728+25442182561159k.
Pour k=0, on a: t=25285696305728
d'où:
N=639366437665582483934527177
est divisible par:
D= 25442182561159=7*13*19*31*37*43*61*67*73, et:
N/D=25130172544303.
De plus, N/D n'est divisible pas aucun des 9 nombres premiers 7, 13, 19,.31, 37, 43, 61, 67, 73.
Donc les puissances de ces nombres premiers dans N sont toutes 1.

Une réponse au problème est donc N=639366437665582483934527177.

Magnifique : c'était ça que je voulais!

Ceci dit, il me semble qu'il y a une règle pour produire les nombres premiers qui vérifient la relation que l'on veut, alors que là je me suis aidé de pari pour factoriser les polynomes dans les corps premiers. Cette démarche est donc ad hoc, donc pas forcément satisfaisante au point de vue théorique.
Mais elle fournit une solution

Moi j'ai fait autrement: par exemple
19|N 7|t²-16t+9 19|(t-8)²-55 (t-8)²=-2 modulo 19.

Le problème a une solution ssi -2 est un carré modulo 19 et tu as la loi de réciprocité quadratique qui répond à ça.

Merci pour tout.

[memphisto]

Yep je sais mais comme j'étais plus sur les extensions algébriques en ce moment, j'ai déliré là dessus... ^^
Il est clair que la loi de réciprocité quad. y répond aisément.

[memphisto]

Pour etre complet:
N/D=25130172544303=1602943*15677521, d'où la décomposition de N en produit de facteurs premiers:
N=7*13*19*31*37*43*61*67*73*1602943*15677521.