Extremum fonction de 3 variables a valeur dans R

[dimou]

Salut,
Alors l'enoncé est le suivant:
Soit q une fonction definie sur R3 par q(x,y,z)=5x²+5y²+6z²+2xy+8xz+8yz
a) Montrer que q ne prend que des valeurs strictement positives sur R3-{0}
b)Soit f(x,y,z)=q(x,y,z)/(x²+y²+z²) def sur R3-{0}
Montrez que f est bornée et atteint ses bornes. Les déterminer!

Pour la question a je m'en suis sorti avec un changement de base en utilisant le fait que q(x,y,z)=tXMX en diagonalisant M qui est une mat symetrique comme pour les coniques a peu pres en trouvant que les valeurs propres sont positives.

Le probleme est pour la b j'essai de calculer quand le grad de f s'annule mais ce sont des calculs tres compliqués.
N'y aurais t'il pas une autre solution?
Merci d'avance

[GaBuZoMeu]

La fonction q est une forme quadratique (comme son petit nom l'indique). La décomposition en carrés de Gauss en montre le caractère défini positif (c'est plus simple que de diagonaliser !).
On peut remarquer que pour tout 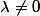. Il suffit donc de regarder ce qui se passe sur la sphère unité.

[dimou]

Dac dac merci du coup de pouce!
j'avais remarque ca en passant en sphérique pour regarder ce qui se passe en 0 qd je faisais des petits test, mais j'avais pas pensé a l'étudier a une distance donnée de l'origine mrc du coup!
Et est-ce que a part un exo comme ca ya d'autres cas typiques de fonction a 3 variables?
(Désolé pour les questions en masses mais bon avec le confinement on a plus de prof... et dans le livre jaune que des fonctions a 2 variables)