Extrema de xyz-ln(x+y+z)

[acteon]

Bonjour,
je dois chercher les éventuels extremas locaux de cette fonction ( x>0, y>0, z>0)
J'ai fait la recherche de point critique, j'ai trouvé B= (a,a,a) avec a= racine cubique de 1/3 mais ensuite je n'arrive pas à conclure. J'ai essayé de m'éloigner un peu de B pour trouver f(x,y,z) - f(B) qui change de signe même infiniment proche de B, mais je n'ai pas trouvé de bon contre exemple.
Ou au contraire de trouver que f(a+h, a+k, a+l) - f(a,a,a) ne change pas de signe quand h, k, l petits mais je n'ai rien de simple non plus.
Vous avez une idée? Dans notre cours nous n'avons pas vu les formes quadratiques ni la hessienne.
Merci pour votre aide!
Remarque: j'ai regardé un peu xy-ln(x+y) mais ce n'est pas beaucoup plus simple.

[GaBuZoMeu]

Peut être regarder regarder ce qui se passe pour la fonction en question
d'une part en restriction à l'intersection de la droite x=y=z avec l'orthant positif
d'autre part en restriction à l'intersection du plan x+y+z=3a avec l'orthant positif.

[acteon]

Merci pour ta réponse même si malheureusement je ne la comprends pas bien, notamment car je ne sais pas ce qu'est l'orthant positif.
ça doit donc pouvoir se traiter sans , mais ça me donnera l'occasion de me renseigner et d'apprendre qqch, merci!

[GaBuZoMeu]

T'inquiète pas, l'orthant positif c'est juste {(x,y,z) | x>0 et y>0 et z>0}

Orthant

[acteon]

ha ok, rien de spécial alors d'autant que les extremas sont cherchés sur cet orthant justement, c'est dans l'énoncé.
Quelqu'un a une autre piste?

[GaBuZoMeu]

Quelqu'un a une autre piste?

Tu pourrais peut-être déjà essayer celle que je t'ai donnée, non ?

Tu as ton point critique (a,a,a). C'est aussi un point critique pour les restrictions, bien sûr. Tu pourrais voir la nature du point critique de la restriction à la droite, et la nature du point critique de la restriction au plan.

[aviateur]

Bonjour
A mon avis il suffit de montrer que ce point n'est pas un extremum.
C'est assez facile d'y arriver il suffit de choisir 2 directions où l'accroissement de f
n'est pas le même.
Assez logiquement tu peux prendre comme direction
ce qui donne
(faire le DL pour trouver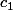 son signe surtout).
Après tu prends une autre direction (pas (0,1,0) à cause des symétries) .
Par exemple
ce qui donne
(faire le DL pour trouver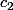 son signe surtout).
Normalement si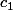 et 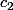de signes contraires tu as fini.

[acteon]

GaBuZoMeu: oui pardon, je m'étais fixé sur cette histoire d'orthant positif et avais oublié que tu proposais une méthode. j'ai commencé à regarder f(x,x,x) et f(x,y, 3a-x-y) avant de m'endormir.
aviateur: merci! je ne sais pas ce qui m'a pris, je n'avais testé que des directions "positives", alors que bien sûr, ce n'est pas parce qu'on travaille dans R^+* ^3 qu'on ne peut pas se déplacer dans toutes les directions, c'est même le principe d'un ouvert!
tes exemples fonctionnent en effet.

Merci à vous deux

[GaBuZoMeu]

Il y a une symétrie dans la fonction, il est naturel de la respecter.
La fonction est facile à étudier. Et si on se restreint au plan , on est amené à se demander où est le maximum de 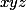pour et de somme constante ; un grand classique, lié à l'inégalité arithmético-géométrique.