Extrema locaux

[w79exz]

Bonjour,
Je dois étudier les extrema locaux de
J'ai fait la hessienne
Et j'ai trouvé H1=2>0, H2=32>0 et H3=-640<0
et grad f = =0
Je n'arrive pas à trouver mes x, y, z pour conclure, est-ce que quelqu'un peut m'aider svp?

[GaBuZoMeu]

Bonjour,

Que veux-tu dire ?
Tu te retrouves dans une situation analogue à celle déjà rencontrée dans ta question sur ilemaths. avec une hessienne qui n'est pas définie, ici de signature (2,1).

[w79exz]

Comment je peux faire pour conclure ?

[GaBuZoMeu]

Te reporter à ton cours.

Ces exercices sont bien dans le cadre d'un cours, n'est-ce pas ?
Tu dois avoir dans ton cours les résultats qui permettent d'étudier les points critiques des fonctions de plusieurs variables. L'outil fondamental est la signature de la matrice hessienne en un tel point critique.

Dans tes exercices, tu as des polynômes du second degré. La hessienne est constante dans ce cas, c'est le double de la matrice de la partie quadratique de l'équation. Si cette partie quadratique est non dégénérée, il y a un unique point critique et sa nature est donnée par la signature de cette forme quadratique : minimum (global) si cette forme quadratique est définie positive, maximum global si elle est définie négative; pas d'extremum dans les autres cas.

Ce que je te dis est très rapide. Ce n'est pas le lieu ici de faire un cours. Une nouvelle fois, je te renvoie au cours que tu as.

[mathelot]

bonsoir,
le gradient s'annule au point A(13/8,-3/8,7/4)

[Black Jack]

Recherche point singulier :

2x + 2y - 6z + 8 = 0 ( )
2x + 18y + 2z = 0 ( )
-6x + 2y + 2z + 7 = 0 ( )

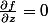
x = 1,625 = 13/8
y = -0,375 = -3/8
z = 1,75 = 7/4

Point singulier : P(13/8 ; -3/8 ; 7/4)

[w79exz]

D'accord merci !

[mathelot]

soit où

après calculs, il vient



il n'y a donc aucun extremum local.