Extensions

[rain]

Bonsoir, quelqu'un pourrait m'expliquer pourquoi Q(racine(3),racine(2))=Q(racine(2)+racine(3)), en utilisant que c'est une extension séparable de Q donc quelle a un élément primitif?

[yos]

Le fait que possède un élément primitif peut se voir sans le théorème de l'élément primitif. D'ailleurs c'est préférable car le théorème en question est un théorème d'existence, qui n'est pas très effectif.
Ici tu as juste à prouver que et . Ce qui peut se voir en prenant l'inverse de par exemple.

[rain]

L'inverse c'est ,mais je vois pas en quoi ça prouve quoi que se soit.

[Doraki]

Ben ça prouve que est dans
Encore un petit effort pour obtenir et

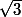
Alternativement, on peut dire que le degré de sur Q c'est 4, qu'il contient , dont le degré sur Q n'est pas 2 ni 1.
Donc ces deux corps sont égaux.

[rain]

je vois pas comment déduire que est dans ,je sens que c'est évident mais je vois pas.

[yos]

Additionne et .