Extensions algébriques.

[matheuxendetresse]

Salut: )

Question de cours:
Si on a algébrique sur l'extension .
A-t-on cette propriété (démo?)
Si est finie (donc algébrique), alors est algébrique sur .

Mercii

[Ben314]

Salut,
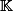
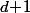
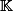
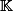
Oui, et c'est évident : dire que est une extension finie, ça veut exactement dire que est un -e.v. de dimension finie donc la famille de qui contient éléments est forcément -liée (propriété basique des e.v. de dim. finie) ce qui signifie qu'il existe non tous nuls tels que donc que est algébrique sur avec un degré .

[matheuxendetresse]

Salut,
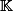
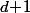
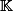
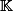
Oui, et c'est évident : dire que est une extension finie, ça veut exactement dire que est un -e.v. de dimension finie donc la famille de qui contient éléments est forcément -liée (propriété basique des e.v. de dim. finie) ce qui signifie qu'il existe non tous nuls tels que donc que est algébrique sur avec un degré

MERCI BIEN,
Oui, ça me semblait naturel, mais je voyais pas comment la prouver.