Exprimez x en fonction de y (chapitre exp. et log.) Quinet tome 1

[tchemerketav]

Merci de votre aide... Je me remets aux mathématiques après 35 ans "d'inactivité"...
Et là je sèche...

y = sin(1/(1-x^2)^1/2)

Je risque d'avoir très souvent besoin d'aide... Pour éviter de vous déranger quelqu'un sait-il si il existe un corrigé de ces exercices : "Cours élémentaire de mathématiques supérieures..." et où se le procurer... ???


Merci par avance.

[zygomatique]

salut

cherche sur internet la fonction arcsin ....

si -1 =< y =< 1 alors tu sais qu'il existe des réels u tels que sin(u) = y

alors 1/(1 - x^2)^(1/2) = u + k2pi ou = pi - u + k2pi avec k entier relatif

ensuite on élève au carré , on passe à l'inverse et on se retrouve avec une équation du second degré en x ....

[tchemerketav]

Oui, c'était ma première intention (arcsin) mais... je m'interdisais cette piste... car cet exercice est partie... voir mon titre... d'un chapitre intitulé : exp. et log... J'avais peur d'avoir loupé quelque chose... On va donc arrêter de se focaliser sur exp. et log... et regarder (cela va être une nouvelle paire de manche) cette "transposition"...

Merci...
Je m'y "recolle" demain...

[paquito]

Ta fonction est paire et définie sur ]-1, 1[, donc elle n'est pas inversible! de plus, quand x->1 y prend une infinité de fois toutes les valeurs comprise entre -1 et 1; en 0 y=sin(1) et finalement, il n'existe aucun intervalle de R sur lequel f est injective et donc arcsin (f(x) n'a aucun sens!!

[Ben314]

...donc arcsin (f(x) n'a aucun sens!!

Bien sûr que si ça a du sens.
Ce que tu est en train de dire, c'est aussi malin que de dire que n'a pas de sens du fait que l'équation a de multiples solutions dans R.
Plus précisément, autant il est vrai que a de multiples solutions dans R, autant on a défini une bonne fois pour toute la fonction racine carrée comme étant LA solution positive de l'équation en question.

Tu réfléchira 15 seconde pour voir que c'est exactement la même chose pour arcsin, plus précisément le même problème et... la même solution adoptée : prendre conventionnellement UNE des solutions que l'on appelle arcsin(truc).
Et, exactement comme pour la racine carrée, il faut savoir quelle est la convention communément admise pour savoir combien vaut le bidule en question.

Enfin, exactement comme pour la fonction racine carrée où on n'a pas , on n'aura pas non plus

[paquito]

Tout élément de ]-1; 1[ a une infinité d'antécédents ; but du jeu?

PS: j'ai réfléchi 1 s. :lol3:

[Ben314]

Tout élément de ]-1; 1[ a une infinité d'antécédents ; but du jeu?

Le même que lorsque l'on définit la fonction racine carrée : gagner un peu de temps en évitant d'avoir à écrire de multiples fois "soit x une des racines carrées de y" : on a décidé une fois pour toute qu'on appellerais LA racine carré de y (réel positif) celle des deux racines carrée qui est positive de façon a avoir effectivement une application (univoque) racine carrée. Par contre, toujours aussi conventionnellement, on évite de le faire dans C vu qu'on perdrait une immense partie des propriétés algébrique que la fonction racine carré as dans R (mais certains auteurs le font quand même en parlant de "détermination principale")

Là, c'est pareil, c'est pratique d'avoir une convention concernant qui on va appeler LE "antécédent privilégié" de y (dans [-1,1]) par la fonction sinus. Cette convention est aussi pratique au niveau des calculatrices et autres ordinateurs pour savoir quel unique valeur ça va renvoyer lorsque l'on tape sur "INV-SIN" (c'est assez pratique que ça renvoie le même résultat conventionnel sur toute les machines)

Bilan : c'est des convention bien pratiques pour alléger la rédaction, mais pour pas mal d'étudiants pas trop bien dégrossis, c'est des vrais "pièges à con" : je te dit pas combien t'écrivent au collège puis au Lycée (voire encore au delà) que puis rebelote dans le supérieur avec puis de même avec (tous faux en général et tous pour la même raison : les fonction x->x² ; x->tan(x) et x->sin(x) ne sont pas bijectives sur leur domaine de définition)

[paquito]

@Ben,

Je comprends parfaitement ton point de vue. C'est exprimer x en fonction de y qui me gêne; sinon, je suis d'accord avec toi, donner en khôles l'étude de x->arcsin(sin(x)) sur R est toujours désespérant :mur:

Je ne sais pas comment tu fais pour coller une figure dans ton post, parce que si l'on regarde les courbes de, de et celle de , on est en droit de se poser pas mal de questions! :lol3:

[Ben314]

Si c'est pour dire que la fonction "à inverser" est pas bien régulière et/ou ne semble pas vraiment correspondre à un truc classique, je suis évidement d'accord, mais la question posée a tout de même "du sens" et on sait le faire.
il me semble que le but de l'exo. c'est uniquement d'apprendre à "inverser" mécaniquement les égalités de la forme et 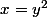et c'est tout.

[paquito]

Inverser mécaniquement???? Je croyais qu'on faisait des maths! x=ln(-y^2) ,-e^x=y^2, y=(-e^x)^1/2......

Il y a quand même quelques précautions à prendre, même si je suis d'accord avec toi, on peut inverser f en prenant les restrictions adéquates. :salut:

[Ben314]

Ben justement, vu qu'on fait des maths, comme tu dit, ça veut dire qu'il faut savoir écrire exactement quelle sont les solution de 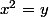et/ou de dans un contexte absolument quelconque, ce qui est le cas ici.
Donc il n'y a rien à "réfléchir" concernant l'utilisation des propriétés particulières de f (vu qu'elle en a pas) mais simplement à "inverser mécaniquement" morceau par morceau (donc le sinus, puis la racine, puis le carré).

Par exemple, par rapports aux aneries que tu as écrit, ça veut dire utiliser mécaniquement :

Perso, je considère pas que "d'utiliser mécaniquement quelque chose" ça veuille dire "utiliser mécaniquement un truc faux"...

Si je te dit par exemple que la simplification d'opération sur des fractions, je fait ça "mécaniquement", pour toi, ça veut forcément dire que je me goure et que j'écris n'importe quoi ?
Pour moi, c'est le contraire que ça veut dire, par exemple, mécaniquement, je vérifie que les truc par lesquels je divise sont non nuls : c'est automatique, systématique et ne me demande aucune réflexion.

[paquito]

Tu as toujours raison! Bien sûr qu'on fait plein de chose mécaniquement, mais d'un point de vu pédagogique, avant que le mécanisme opère, il y a du boulot.
Les "âneries" que j'ai écrite, les collègues qui ont une TS en voient plein tous les jours; exemples:




, etc....

Tiens, peut tu me donner en valeur exacte le réel tel que la restriction de à soit une bijection, le réel étant maximal? :lol3:

[Ben314]

Donc sur où est la plus petite solution >0 de et, comme est croissante sur ]0,1[, c'est que c'est à dire

[paquito]

Bien joué Ben! :we: