Pour revenir, en effet un peu à ta question initiale. Pour trouver l'expression du terme général d'une suite donnée par une relation de récurrence, on a souvent recourt à deux techniques :
1) le changement de variable pour simplifier la récurrence
2) les séries formelle ou fonction génératrice
1) Changement de variableici c'est
^n}{n!}u_n)
d'où les premières expressions obtenus en sommant
^n}{(n+1)!}e^2)
soit
^n}{n!}u_n = -\frac{1}{2} + \frac{e^2}{2} \bigsum_{k=0}{n}{\frac{(-2)^k}{k!}})
la somme c'est les n+1 premiers termes du développement en série de taylor de e^(-2), en notant
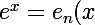 + r_n(x) = \bigsum_{k \le n}{\frac{x^n}{n!}} + \bigsum_{k \gt n}{\frac{x^n}{n!}})
soit
^n}{n!}u_n = - \frac{e^2}{2}r_n(-2)) 2) La série génératrice
2) La série génératriceon peut utiliser des séries formelles pour résoudre la récurrence, il s'agit en gros de trouver une équation différentielle ou fonctionnelle dont les solutions ont pour développement en série entière :
=\bigsum_{n \ge 0} u_nX^n)
ou
=\bigsum_{n \ge 0} \frac{u_n}{n!}X^n)
ici c'est le deuxième cas qui est intéressant :
u_n = e^2)
!}X^{n+1} + X \frac{u_n}{n!}X^n = \frac{e^2}{(n+1)!}X^{n+1})
-f(0)) + Xf(X) = e^2(e^X-1))
finalement
 = \frac{e^{2+X}-1}{2+X})
comme je l'avais déjà trouvé
et on à bien du faite du développement en série de taylor
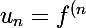}(0))
voilà il y a certainement des tas d'autres approches mais elles donnent toute le même résultat (encore heureux!)
D'un autre côté, du point de vue mathématique ça ne sert souvent à rien d'avoir l'expression explicite on ce contente bien souvent d'un équivalent ou d'un développement asymptotique. Qui vont suffire à déterminer la limite et sa vitesse d'approche.