Bonjour,
Je vous soumets un exo de probas donné à l'oral d'Ulm en section B/L en 2004.
Je n'arrive pas à faire la question 3 et j'en viens à penser qu'elle est fausse.
Il est peut-être possible d'obtenir une majoration similaire...
Soit X_{1},...,X_{k},... des variables aléatoires
indépendantes de loi de Bernoulli de paramètre p. Soit
N une variable aléatoire indépendante des variables
aléatoires de Bernoulli précédentes suivant une loi de
Poisson de paramètre entier n>= 1. Pour tout entier
k>=1, on pose S_{k}=X_{1}+...+X_{k}.
On définit de plus S_{0}=0.
1. Calculer la loi de la variable aléatoire S_{N}.
2. Vérifier que E(S_N-S_n) =0.
3. Etablir que E((S_N-S_n)^2) <=sqrt{n}p(1-p)
4. En déduire que pour tout epsilon > 0 et tout
alpha\in ] 0, 3/4 [ ,
\lim_{n\rightarrow\infty}P(n^{alpha}|S_N/n-S_n/n| >=epsilon) =0
PS. Est-ce qu'on peut taper des maths en utilisant latex sur ce forum et est-ce que c'est expliqué quelque part ?
Exo Ulm section B/L
4 messages
- Page 1 sur 1
michal a écrit:PS. Est-ce qu'on peut taper des maths en utilisant latex sur ce forum et est-ce que c'est expliqué quelque part ?
Oui, tu peux voir ici http://www.maths-forum.com/showthread.php?t=3414
Soit  des variables aléatoires
des variables aléatoires
indépendantes de loi de Bernoulli de paramètre . Soit
. Soit
 une variable aléatoire indépendante des variables aléatoires de
une variable aléatoire indépendante des variables aléatoires de
Bernoulli précédentes suivant une loi de Poisson de paramètre entier .
.
Pour tout entier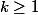 , on pose
, on pose
 . On définit de plus
. On définit de plus  .
.
1. Calculer la loi de la variable aléatoire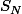 .
.
2. Vérifier que=0) .
.
3. Etablir que^{2}\right) \leq \sqrt{n}p\left(1-p\right)) .
.
4. En déduire que pour tout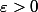 et tout
et tout
 ,
,
=0)
c'est quand même plus beau...
indépendantes de loi de Bernoulli de paramètre
Bernoulli précédentes suivant une loi de Poisson de paramètre entier
Pour tout entier
1. Calculer la loi de la variable aléatoire
2. Vérifier que
3. Etablir que
4. En déduire que pour tout
c'est quand même plus beau...
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
