Exo théorie des corps !

[barbu23]

Bonjour à tous : :happy3:
J'ai un autre exo à resoudre, le voiçi :
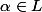
Soit une extension d'un corps et algebrique de degré impair .
Montrer que
Meric de votre aide ! :happy3:

[barbu23]

J'ai une autre question à vous poser : :happy3:
Pourquoi si et sont algebrique dans sur alors, l'est aussi !
MErci de votre aide ! :happy3:

[Doraki]

Voici un autre exo plus important qui risque de te servir :
Soit K un corps, L une extension de K de degré d, L' une extension de L de degré d'.
Montrer que L' est une extension de K de degré (d*d') en expliquant comment obtenir une K-base de L' à partir d'une K-base de L et d'une L-base de L'.

[barbu23]

Voici un autre exo plus important qui risque de te servir :
Soit K un corps, L une extension de K de degré d, L' une extension de L de degré d'.
Montrer que L' est une extension de K de degré (d*d') en expliquant comment obtenir une K-base de L' à partir d'une K-base de L et d'une L-base de L'.

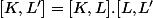
ça c'est un exo qui relève de la theorie de l'algèbre linéaire : ( Je connais ce theorème car je l'ai dèjà vu dans mon cours ) :happy3: ( la base c'est )

[yos]

Tu achèves en remarquant que est une extension de de degré au plus 2.

[yos]

Pour l'autre question (somme de deux algébriques), tu as le résultat plus fort qui dit que les éléments de L algébriques sur K forment un corps. Tu dois avoir ça dans ton cours. Trouver un polynôme annulateur de a+b connaissant des polynômes annulateurs de a et de b est pas simple en général.

[Ben314]

Pour l'algébricité (ca se dit ca ???) de alpha+beta ou de alpha.beta, en théorie c'est pas super dur : tu raisonne dans une famille génératrice d'un corps contenant alpha et beta (si alpha et beta sont algébriques de degrés respectifs n et m, l'ensembles de alpha^i.beta^j avec 0<=i<n et 0<=j<m fait trés bien l'affaire).
Dans cette base, tu écrit les coordonnées de 1,(alpha+beta),(alpha+beta)^2.... (idem pour le produit) jusqu'à ce que la famille soit liée (ce qui arrivera forcément puisqu'on est en dimension finie) et tue en déduit un polynôme qui annule alpha+beta.
Dans les bon cas (si base + on s'arrète au premier cran ou la famille est liée) on a le poly minimal.

Exercice :
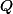
Déterminer le polynôme minimal (sur ) de .