Exo structure
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
singular
- Membre Naturel
- Messages: 34
- Enregistré le: 29 Sep 2008, 20:38
-
 par singular » 18 Fév 2009, 20:30
par singular » 18 Fév 2009, 20:30
Bonjour sauriez vous m'aidez pour résoudre
l'équation suivante:
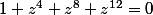
En sachant que c'est la dernière question de mon exercice:
on m' a d'abord demandé de:
-résoudre sur

l'équation (E):
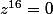
.
-après en considérant G l'ensemble des solution de (E), j'ai montré que G était u groupe commutatif pour la multiplication.
-
on m'a demandé ensuite de calculer la somme des éléments de G.
Alors là il est vrai que je ne suis pas tout à fait sûr de moi parce que j'ai juste dit que par définition on a la relation:
 mais je ne fait aucun calcul !
mais je ne fait aucun calcul !je vous remercie de m'aidez au plus vite.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 18 Fév 2009, 20:50
par skilveg » 18 Fév 2009, 20:50
Déjà, je pense que c'est plutôt l'équation
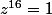
... A partir de là, c'est une somme géométrique: tu as l'identité
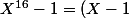\sum_{k=0}^{15}X^k)
ce qui te permet de conclure sachant que le groupe dont tu parles est cyclique (par exemple engendré par la racine primitive seizième
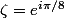
).
(D'ailleurs, je ne vois pas pourquoi "par définition" on aurait cette relation.)
Autre solution: si tu prends un élément

dans ton groupe, alors

permute le groupe, donc ne change pas la somme; en la notant

, ça donne
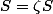
donc
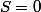
.
-
singular
- Membre Naturel
- Messages: 34
- Enregistré le: 29 Sep 2008, 20:38
-
 par singular » 18 Fév 2009, 23:06
par singular » 18 Fév 2009, 23:06
oui pardonnez moi l'équation (E) est bien:

(D'ailleurs, je ne vois pas pourquoi "par définition" on aurait cette relation.)
En fait le terme est peut être mal choisi, je pensais utiliser le fait que la somme des racines n-ièmes de l'unité est nulle (sinon en utilisant la relation coefficient racine d'un polynôme je ne vois pas, à moins que le coefficient de l'un des
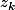
soit nulle)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 18 Fév 2009, 23:12
par leon1789 » 18 Fév 2009, 23:12
singular a écrit:Bonjour sauriez vous m'aidez pour résoudre
l'équation suivante:
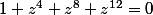
En posant
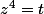
, on arrive à
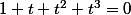
ce qui se factorise en
(...) = 0)
On en déduit les valeurs de t, puis celles de z.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 18 Fév 2009, 23:40
par skilveg » 18 Fév 2009, 23:40
singular a écrit: je pensais utiliser le fait que la somme des racines n-ièmes de l'unité est nulle
OK. Après, à toi de juger si la question implique de le redémontrer ou pas.
Sinon, pour l'équation, on pourrait multiplier par

pour se ramener à ce qui a été fait avant, mais ça me paraît moins naturel que ce que propose Leon.
-
singular
- Membre Naturel
- Messages: 34
- Enregistré le: 29 Sep 2008, 20:38
-
 par singular » 18 Fév 2009, 23:46
par singular » 18 Fév 2009, 23:46
ceci correspondait en fait à la fi de mon exercice
au début j'ai l'équation
:z^{16}-1=0)
que j'ai résolu:
:z^{16}-1=0)




après on me demande de calculer la somme des éléments de G (des
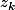
), mais là je bloque, si vous pouviez m'aider.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 20 Fév 2009, 00:46
par skilveg » 20 Fév 2009, 00:46
Qu'est-ce que tu ne comprends pas dans mon premier message?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
