Exo a resoudre par changement de variable simple
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 01 Oct 2015, 10:30
par mathelot » 01 Oct 2015, 10:30
il nous faudrait les données numériques (des questions précédentes)
-
youyou0772
- Messages: 8
- Enregistré le: 01 Oct 2015, 10:18
-
 par youyou0772 » 01 Oct 2015, 10:37
par youyou0772 » 01 Oct 2015, 10:37
mathelot a écrit:il nous faudrait les données numériques (des questions précédentes)
Pardon j'ai modifié la pièce jointe.merci mathelot
-
JaCQZz
 par JaCQZz » 01 Oct 2015, 10:54
par JaCQZz » 01 Oct 2015, 10:54
mathelot a écrit:il nous faudrait les données numériques (des questions précédentes)
Ici, les données desservent l'exo.
On dispose des modèles suivants:
 y= ax^b, \\ 2)y = a + \frac{b}{x}, \\ 3) y = \frac{1}{ax+b} \\ 4) y = \frac{x}{ax+b})
Or, on veut que :

 \in \mathbb{R})
Transforme la formule...
-
youyou0772
- Messages: 8
- Enregistré le: 01 Oct 2015, 10:18
-
 par youyou0772 » 01 Oct 2015, 10:59
par youyou0772 » 01 Oct 2015, 10:59
JaCQZz a écrit:Ici, les données desservent l'exo.
On dispose des modèles suivants:
 y= ax^b, \\ 2)y = a + \frac{b}{x}, \\ 3) y = \frac{1}{ax+b} \\ 4) y = \frac{x}{ax+b})
Or, on veut que :

 \in \mathbb{R})
Transforme la formule...
j'ai pas saisi seulement la deuxième question( deuxième partie la démonstration) pouvez vous m'expliquer
-
JaCQZz
 par JaCQZz » 01 Oct 2015, 11:04
par JaCQZz » 01 Oct 2015, 11:04
youyou0772 a écrit:j'ai pas saisi seulement la deuxième question( deuxième partie la démonstration) pouvez vous m'expliquer
Vous avez enlevé l'exercice qui figurait à son public. Rectifiez aussi un x par le X (changement de variable).
-
youyou0772
- Messages: 8
- Enregistré le: 01 Oct 2015, 10:18
-
 par youyou0772 » 01 Oct 2015, 11:20
par youyou0772 » 01 Oct 2015, 11:20
JaCQZz a écrit:Vous avez enlevé l'exercice qui figurait à son public. Rectifiez aussi un x par le X (changement de variable).
Merci JaCQZz pour aimable attention.s'est fait.pouvez vous me donner des clarification a propos de la deuxième partie
-
JaCQZz
 par JaCQZz » 01 Oct 2015, 11:32
par JaCQZz » 01 Oct 2015, 11:32
L'exo s'apparente a posteriori à une régression linéaire.
Un modèle affine est :
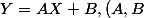 \in \mathbb{R})
Pour le 1) par ex, on aura le résultat avec :

-
youyou0772
- Messages: 8
- Enregistré le: 01 Oct 2015, 10:18
-
 par youyou0772 » 01 Oct 2015, 11:36
par youyou0772 » 01 Oct 2015, 11:36
JaCQZz a écrit:L'exo s'apparente a posteriori à une régression linéaire.
Un modèle affine est :
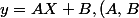 \in \mathbb{R})
Pour le 1) par ex, on aura le résultat avec :

et concernant l'identification de paramètres a et b
-
youyou0772
- Messages: 8
- Enregistré le: 01 Oct 2015, 10:18
-
 par youyou0772 » 01 Oct 2015, 11:41
par youyou0772 » 01 Oct 2015, 11:41
JaCQZz a écrit:L'exo s'apparente a posteriori à une régression linéaire.
Un modèle affine est :
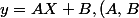 \in \mathbb{R})
Pour le 1) par ex, on aura le résultat avec :

le changement de variable
Y = ln y , X = x , A = ln a , B = ln b
-
JaCQZz
 par JaCQZz » 01 Oct 2015, 11:51
par JaCQZz » 01 Oct 2015, 11:51
Au fait, applique juste :
 = ln{a}+ ln(x^b) = ln{a} + bln{x})
J'ai modifié: y par Y. plus haut. Or, tu as été trop rapide à linéariser la formule...
On obtient alors suite à cette transformation :

-
youyou0772
- Messages: 8
- Enregistré le: 01 Oct 2015, 10:18
-
 par youyou0772 » 01 Oct 2015, 14:31
par youyou0772 » 01 Oct 2015, 14:31
JaCQZz a écrit:Au fait, applique juste :
 = ln{a}+ ln(x^b) = ln{a} + bln{x})
J'ai modifié: y par Y. plus haut. Or, tu as été trop rapide à linéariser la formule...
On obtient alors suite à cette transformation :

Merci , bien entendu
-
youyou0772
- Messages: 8
- Enregistré le: 01 Oct 2015, 10:18
-
 par youyou0772 » 01 Oct 2015, 14:39
par youyou0772 » 01 Oct 2015, 14:39
on peut verifier la première partie ensemble.je vais te donner ma solution .réponds moi
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
