Exo proba
24 messages
- Page 1 sur 2 - 1, 2
exo proba
Un base de données contient 2n n° de matricule : n de femmes et n d'hommes Pour constituer un couple il faut une homme et une femme.
On tire, avec remise, parmi ces 2n n° de matricules jusque la formation d'un couple.
Soit X la variable aléatoire egale au nombre de tirage nécessaire pour obtenir un couple.
Déterminer la loi de X !
J'ai du mal à dénombrer et donc à trouver X ! :hum:
une idée ?!
On tire, avec remise, parmi ces 2n n° de matricules jusque la formation d'un couple.
Soit X la variable aléatoire egale au nombre de tirage nécessaire pour obtenir un couple.
Déterminer la loi de X !
J'ai du mal à dénombrer et donc à trouver X ! :hum:
une idée ?!
Salut
Pour former un couple il faut tirer un numéro parmi les n numéros du sexe opposé au premier numéro, c'est-à-dire un des n numéros sur 2n-1
A chaque tirage, on a une probabilité de former un couple.
de former un couple.
X représente le nombre de tirages qu'il faut effectuer pour former un couple (succès), c'est une loi géométrique.
 =\frac{n}{2n-1} = p) et
et =\frac{n-1}{2n-1})
 = p \, (1-p)^{k-1}) (p est la probabilité de succès)
(p est la probabilité de succès)
Pour former un couple il faut tirer un numéro parmi les n numéros du sexe opposé au premier numéro, c'est-à-dire un des n numéros sur 2n-1
A chaque tirage, on a une probabilité
X représente le nombre de tirages qu'il faut effectuer pour former un couple (succès), c'est une loi géométrique.
Bonsoir,
C'est effectivement très simple mais pas tout à fait ce qu'a ecrit sdec25 :
Notons p= proba de sortir une femme et q =proba de sortir un homme.
Pour obtenir un couple au bout de k>1 tirages, il faut :
Donc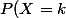=p^{k-1} q + q^{k-1} p=pq[p^{k-2}+q^{k-2}])
Avec p=q=0,5 cela donne 2(p^k)
Si k<2 alors P(X=k)=0
C'est effectivement très simple mais pas tout à fait ce qu'a ecrit sdec25 :
Notons p= proba de sortir une femme et q =proba de sortir un homme.
Pour obtenir un couple au bout de k>1 tirages, il faut :
- tirer k-1 femmes puis un homme :
ou - tirer k-1 hommes puis une femme :
Donc
Avec p=q=0,5 cela donne 2(p^k)
Si k<2 alors P(X=k)=0
maintenant à partir du meme problème on effectue un tirage sans remise et donc la machnie retire les n° déja tirés (de sorte à ne pas tirer 2 fois le meme n°)
On a T la variable aléatoire égale au nombre de tirages nécessaires pour former un couple.
1) Calculer la proba que les k premieres personnes soient du meme sexe en fonction de n et k
2) Calculer la proba que T>k en fonction de n et k et la comparer à ... et en déduire la loi de T
... et en déduire la loi de T
pour la 1 : je pense à!}{(n-k)!(2n)!}})
pour le reste j'ai du mal !
On a T la variable aléatoire égale au nombre de tirages nécessaires pour former un couple.
1) Calculer la proba que les k premieres personnes soient du meme sexe en fonction de n et k
2) Calculer la proba que T>k en fonction de n et k et la comparer à
pour la 1 : je pense à
pour le reste j'ai du mal !
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
